《2025年暑期升级训练七年级数学浙教版浙江教育出版社》

1. 下列语句中,属于定义的是 ()

A.直线a和b垂直吗
B.两点确定一条直线
C.两直线平行,内错角相等
D.整数与分数统称为有理数

答案： #### 预学训练
1. D

2. 给出下列语句：① 两直线相交,只有一个交点；② 过点P画直线AB的垂线；③ 延长线段AB到点C；④ 整数都能被2整除。其中,命题的个数为 ()

A.1
B.2
C.3
D.4

答案： 2. B

3. 下列四个命题中,属于真命题的是 ()

A.两直线平行,同旁内角相等
B.如果$x^{2}＞0$,那么$x＞0$
C.若两条直线不平行,则这两条直线一定垂直
D.$\sqrt{81}的平方根是\pm3$

答案： 3. D

4. 下列说法中,正确的是 ()

A.命题是定理,但定理未必是命题
B.基本事实和定理都是真命题
C.定理和命题一样,有真有假
D.“取线段AB的中点C”是一个真命题

答案： 4. B

5. 命题“垂直于同一条直线的两条直线平行”的条件是 ()

A.垂直
B.两条直线
C.同一条直线
D.两条直线垂直于同一条直线

答案： 5. D

6. 要说明命题“两个数相加,和一定大于其中一个加数”是假命题,能够作为反例的是 ()

A.$1+3= 4$
B.$-1+3= 2$
C.$0+3= 3$
D.$-1+(-3)= -4$

答案： 6. D

7. (教材P15作业题第2题变式)写出二元一次方程组的定义：____。

答案： 7. 由两个一次方程组成，并且含有两个未知数的方程组，叫作二元一次方程组

8. (教材P15作业题第5题变式)把命题“互为相反数的两个数的和为零”改写成“如果……那么……”的形式：____。

答案： 8. 如果两个数互为相反数，那么这两个数的和为零

9. 命题“若$ab= 0$,则$a= b= 0$”是____命题(填“真”或“假”)。

答案： 9. 假

10. (1)判断下列语句是不是命题,若是,写成“如果……那么……”的形式,并判断其是真命题还是假命题。
① 同位角相等,两直线平行。
② 画两条相等的线。
(2)举反例说明下列命题是假命题：
① 相等的角是同位角。
② 大于$90^{\circ}$的角为钝角。

答案： 10. （1）① 是命题，写成“如果……那么……”的形式如下：如果两条直线被第三条直线所截得的同位角相等，那么这两条直线平行. 是真命题. ② 不是命题. （2）答案不唯一，如① 反例：对顶角相等，但不是同位角. ② 反例：$180^{\circ}$的角不是钝角.

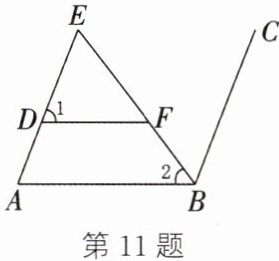
11. 如图,$∠1+∠ABC= 180^{\circ}$,给出下列三个条件：① BE是$∠ABC$的平分线；②$∠E= ∠2$；③$DF// AB$。请你从中选出两个作为已知条件,另一个作为结论,组成一个真命题,并加以证明。

答案： 11. 选择不唯一，如条件是①②，结论是③. 因为$BE$是$\angle ABC$的平分线，所以$\angle 2 = \angle CBE$. 因为$\angle E = \angle 2$，所以$\angle CBE = \angle E$. 所以$AE // BC$. 所以$\angle A + \angle ABC = 180^{\circ}$. 因为$\angle 1 + \angle ABC = 180^{\circ}$，所以$\angle A = \angle 1$. 所以$DF // AB$.