2025年暑假总动员七年级数学沪科版合肥工业大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假总动员七年级数学沪科版合肥工业大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第64页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
5. 如图,已知AB//CD,∠A=54°,∠E=18°,则∠C的度数是( )
A. 36° B. 34° C. 32° D. 30°
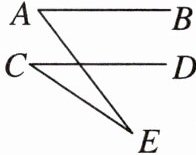
A. 36° B. 34° C. 32° D. 30°

答案:
A [解析]过点$E$作$EF// AB$,则$EF// CD$,如图所示。因为$EF// AB$,所以$∠AEF=∠A=54^{\circ }$,所以$∠CEF=∠AEF - ∠AEC=54^{\circ } - 18^{\circ }=36^{\circ }$。又因为$EF// CD$,所以$∠C=∠CEF=36^{\circ }$。

A [解析]过点$E$作$EF// AB$,则$EF// CD$,如图所示。因为$EF// AB$,所以$∠AEF=∠A=54^{\circ }$,所以$∠CEF=∠AEF - ∠AEC=54^{\circ } - 18^{\circ }=36^{\circ }$。又因为$EF// CD$,所以$∠C=∠CEF=36^{\circ }$。

6. 如图,AB//CD,ME平分∠AMF,NF平分∠CNE,EN,MF交于点O.
(1)若∠AMF=50°,∠CNE=40°,则∠MEN=______°,∠MFN=______°;
(2)若图中∠MEN+60°=2∠MFN,则∠AMF的度数为______;
(3)探究∠MEN,∠MFN与∠MON之间的数量关系.

(1)若∠AMF=50°,∠CNE=40°,则∠MEN=______°,∠MFN=______°;
(2)若图中∠MEN+60°=2∠MFN,则∠AMF的度数为______;
(3)探究∠MEN,∠MFN与∠MON之间的数量关系.

答案:
解:
(1)分别过点$E$,$F$作$AB$的平行线,则它们同时也与$CD$平行,则有$∠MEN=∠AME + ∠CNE$,$∠MFN=∠AMF + ∠CNF$。由$∠AMF=50^{\circ }$,$∠CNE=40^{\circ }$,$ME$平分$∠AMF$,$NF$平分$∠CNE$,得$∠AME=25^{\circ }$,$∠CNF=20^{\circ }$,所以$∠MEN=65^{\circ }$,$∠MFN=70^{\circ }$。
(2)$40^{\circ }$ [解析]由
(1)可知$∠MEN=∠AME + ∠CNE$,$∠MFN=∠AMF + ∠CNF$,则有$∠AME + ∠CNE + 60^{\circ }=2∠AMF + 2∠CNF$。又$2∠CNF=∠CNE$,$2∠AME=∠AMF$,所以$∠AMF=60^{\circ }$,故$∠AMF=40^{\circ }$。
(3)过点$O$作$AB$的平行线,则它同时也与$CD$平行,易证$∠MON=∠AMF + ∠CNE$。因为$∠MEN=∠AME + ∠CNE$,$∠MFN=∠AMF + ∠CNF$,所以$∠MEN + ∠MFN=\frac {3}{2}(∠AMF + ∠CNE)$,所以$∠MEN + ∠MFN=\frac {3}{2}∠MON$。
(1)分别过点$E$,$F$作$AB$的平行线,则它们同时也与$CD$平行,则有$∠MEN=∠AME + ∠CNE$,$∠MFN=∠AMF + ∠CNF$。由$∠AMF=50^{\circ }$,$∠CNE=40^{\circ }$,$ME$平分$∠AMF$,$NF$平分$∠CNE$,得$∠AME=25^{\circ }$,$∠CNF=20^{\circ }$,所以$∠MEN=65^{\circ }$,$∠MFN=70^{\circ }$。
(2)$40^{\circ }$ [解析]由
(1)可知$∠MEN=∠AME + ∠CNE$,$∠MFN=∠AMF + ∠CNF$,则有$∠AME + ∠CNE + 60^{\circ }=2∠AMF + 2∠CNF$。又$2∠CNF=∠CNE$,$2∠AME=∠AMF$,所以$∠AMF=60^{\circ }$,故$∠AMF=40^{\circ }$。
(3)过点$O$作$AB$的平行线,则它同时也与$CD$平行,易证$∠MON=∠AMF + ∠CNE$。因为$∠MEN=∠AME + ∠CNE$,$∠MFN=∠AMF + ∠CNF$,所以$∠MEN + ∠MFN=\frac {3}{2}(∠AMF + ∠CNE)$,所以$∠MEN + ∠MFN=\frac {3}{2}∠MON$。
7. 如果∠1的两边与∠2的两边互相平行,且∠1=60°,那么∠2=______.
答案:
$60^{\circ }$或$120^{\circ }$
8. 一副三角尺按如图所示方式叠放在一起,其中点B,D重合,若固定三角尺AOB,改变三角尺ACD的位置(其中A点位置始终不变),使三角尺ACD的一边与三角尺AOB的某一边平行,则∠BAD的所有可能的值是__________.


答案:
$15^{\circ }$,$30^{\circ }$,$45^{\circ }$,$75^{\circ }$,$105^{\circ }$,$135^{\circ }$,$150^{\circ }$,$165^{\circ }$
[解析]分8种情况讨论:
①如图1,$∠BAD=45^{\circ }$时,$AD$边与$OB$边平行;
②如图2,$∠BAD=135^{\circ }$时,$AC$边与$OB$边平行;
③如图3,$∠BAD=150^{\circ }$时,$DC$边与$AB$边平行;
④如图4,$∠BAD=165^{\circ }$时,$DC$边与$OB$边平行;
⑤如图5,$∠BAD=15^{\circ }$时,$DC$边与$OB$边平行;
⑥如图6,$∠BAD=105^{\circ }$时,$DC$边与$AO$边平行;
⑦如图7,$∠BAD=30^{\circ }$时,$DC$边与$AB$边平行;
⑧如图8,$∠BAD=75^{\circ }$时,$DC$边与$AO$边平行。
(与这8种情况位置不同,且满足题意,但所求出角度与上述8种情况中的一种相同的情况略)



$15^{\circ }$,$30^{\circ }$,$45^{\circ }$,$75^{\circ }$,$105^{\circ }$,$135^{\circ }$,$150^{\circ }$,$165^{\circ }$
[解析]分8种情况讨论:
①如图1,$∠BAD=45^{\circ }$时,$AD$边与$OB$边平行;
②如图2,$∠BAD=135^{\circ }$时,$AC$边与$OB$边平行;
③如图3,$∠BAD=150^{\circ }$时,$DC$边与$AB$边平行;
④如图4,$∠BAD=165^{\circ }$时,$DC$边与$OB$边平行;
⑤如图5,$∠BAD=15^{\circ }$时,$DC$边与$OB$边平行;
⑥如图6,$∠BAD=105^{\circ }$时,$DC$边与$AO$边平行;
⑦如图7,$∠BAD=30^{\circ }$时,$DC$边与$AB$边平行;
⑧如图8,$∠BAD=75^{\circ }$时,$DC$边与$AO$边平行。
(与这8种情况位置不同,且满足题意,但所求出角度与上述8种情况中的一种相同的情况略)



9. (1)如图1,直线AB,CD被直线EF所截,EM平分∠AEF,FM平分∠CFE.若∠AEM=55°,∠CFM=35°,则AB与CD平行吗?请说明理由;
(2)如图2,若直线AB//CD,点M在直线AB,CD之间,点E,F分别在直线AB,CD上,∠EMF=90°,P是MF上一点,且EM平分∠AEP.若∠CFM=60°,则∠AEP的度数为多少;
(3)若直线AB//CD,点E,F分别在直线AB,CD上,点M在直线AB,CD之间,且在直线EF的左侧,P是折线E-M-F上的一个动点,∠EMF=90°保持不变,移动点P,使EM平分∠AEP或FM平分∠CFP.设∠CFP=α,∠AEP=β,请写出α与β之间的数量关系.
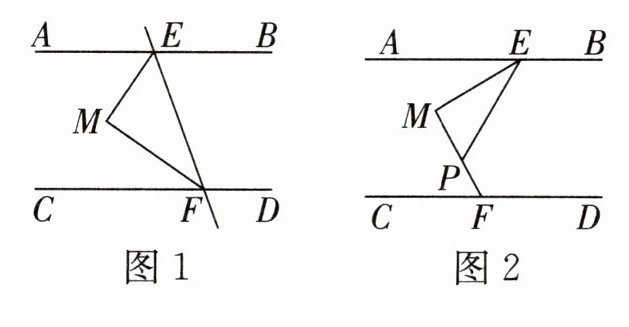
(2)如图2,若直线AB//CD,点M在直线AB,CD之间,点E,F分别在直线AB,CD上,∠EMF=90°,P是MF上一点,且EM平分∠AEP.若∠CFM=60°,则∠AEP的度数为多少;
(3)若直线AB//CD,点E,F分别在直线AB,CD上,点M在直线AB,CD之间,且在直线EF的左侧,P是折线E-M-F上的一个动点,∠EMF=90°保持不变,移动点P,使EM平分∠AEP或FM平分∠CFP.设∠CFP=α,∠AEP=β,请写出α与β之间的数量关系.

答案:
解:
(1)$AB// CD$,理由:因为$∠AEM=55^{\circ }$,$EM$平分$∠AEF$,所以$∠AEF=2∠AEM=110^{\circ }$。因为$∠CFM=35^{\circ }$,$FM$平分$∠CFE$,所以$∠CFE=2∠CFM=70^{\circ }$,所以$∠AEF + ∠CFE=180^{\circ }$,所以$AB// CD$。
(2)如图1,过点$M$作$MN// AB$。因为$AB// CD$,所以$AB// CD// MN$。所以$∠AEM=∠NME$,$∠CFM=∠NMF=60^{\circ }$,所以$∠EMF=∠EMN + ∠NMF=∠AEM + ∠CFM=90^{\circ }$,所以$∠AEM=∠EMN=30^{\circ }$。因为$EM$平分$∠AEP$,所以$∠AEP=2∠AEM=60^{\circ }$。
(3)如图2,若$EM$平分$∠AEP$,则$∠AEM=∠PEM=\frac {1}{2}∠AEP=\frac {1}{2}β$。同
(2),可得$∠EMF=∠AEM + ∠CFP=90^{\circ }$,所以$\frac {1}{2}β+α=90^{\circ }$。如图3,若$FM$平分$∠CFP$,则$∠CFM=∠PFM=\frac {1}{2}∠CFP=\frac {1}{2}α$。同
(2),可得$∠EMF=∠AEP + ∠CFM=90^{\circ }$,所以$β+\frac {1}{2}α=90^{\circ }$。综上所述,$α$与$β$之间的数量关系为$α+\frac {1}{2}β=90^{\circ }$或$β+\frac {1}{2}α=90^{\circ }$。



解:
(1)$AB// CD$,理由:因为$∠AEM=55^{\circ }$,$EM$平分$∠AEF$,所以$∠AEF=2∠AEM=110^{\circ }$。因为$∠CFM=35^{\circ }$,$FM$平分$∠CFE$,所以$∠CFE=2∠CFM=70^{\circ }$,所以$∠AEF + ∠CFE=180^{\circ }$,所以$AB// CD$。
(2)如图1,过点$M$作$MN// AB$。因为$AB// CD$,所以$AB// CD// MN$。所以$∠AEM=∠NME$,$∠CFM=∠NMF=60^{\circ }$,所以$∠EMF=∠EMN + ∠NMF=∠AEM + ∠CFM=90^{\circ }$,所以$∠AEM=∠EMN=30^{\circ }$。因为$EM$平分$∠AEP$,所以$∠AEP=2∠AEM=60^{\circ }$。
(3)如图2,若$EM$平分$∠AEP$,则$∠AEM=∠PEM=\frac {1}{2}∠AEP=\frac {1}{2}β$。同
(2),可得$∠EMF=∠AEM + ∠CFP=90^{\circ }$,所以$\frac {1}{2}β+α=90^{\circ }$。如图3,若$FM$平分$∠CFP$,则$∠CFM=∠PFM=\frac {1}{2}∠CFP=\frac {1}{2}α$。同
(2),可得$∠EMF=∠AEP + ∠CFM=90^{\circ }$,所以$β+\frac {1}{2}α=90^{\circ }$。综上所述,$α$与$β$之间的数量关系为$α+\frac {1}{2}β=90^{\circ }$或$β+\frac {1}{2}α=90^{\circ }$。



查看更多完整答案,请扫码查看


