《2025年暑假总动员七年级数学沪科版合肥工业大学出版社》

12. (1)如图1，已知正方形ABCD的边长为a，正方形FGCH的边长为b，长方形ABGE和EFHD为阴影部分，则阴影部分的面积是______(写成平方差的形式)；
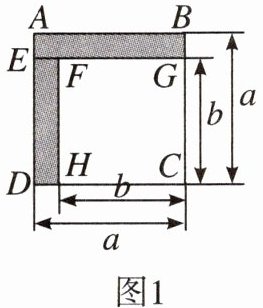
(2)将图1中的长方形ABGE和EFHD剪下来，拼成图2所示的长方形，则长方形FEGB的面积是______(写成多项式相乘的形式)；
(3)比较图1与图2的阴影部分的面积，可得乘法公式______；
(4)计算：$2(1+\frac {1}{2})(1+\frac {1}{2^{2}})(1+\frac {1}{2^{4}})(1+\frac {1}{2^{8}})+\frac {1}{2^{14}}$。

答案： 解：
(1)$a^{2}-b^{2}$
(2)$(a + b)(a - b)$
(3)$(a + b)(a - b)=a^{2}-b^{2}$
(4)原式$=4(1-\frac{1}{2})(1+\frac{1}{2})(1+\frac{1}{2^{2}})(1+\frac{1}{2^{4}})(1+\frac{1}{2^{8}})+\frac{1}{2^{14}}$
$=4(1-\frac{1}{2^{2}})(1+\frac{1}{2^{2}})(1+\frac{1}{2^{4}})(1+\frac{1}{2^{8}})+\frac{1}{2^{14}}$
$=4(1-\frac{1}{2^{4}})(1+\frac{1}{2^{4}})(1+\frac{1}{2^{8}})+\frac{1}{2^{14}}$
$=4(1-\frac{1}{2^{8}})(1+\frac{1}{2^{8}})+\frac{1}{2^{14}}$
$=4(1-\frac{1}{2^{16}})+\frac{1}{2^{14}}$
$=4-\frac{1}{2^{14}}+\frac{1}{2^{14}}$
$=4$.

13. 【知识生成】
我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式。
例如图1可以得到$(a+b)^{2}=a^{2}+2ab+b^{2}$，基于此，请解答下列问题：
(1)如图2是用2个小正方体和6个小长方体拼成的一个大正方体，用不同的方法表示这个大正方体的体积，则可得等式______；
(2)利用(1)中得到的结论，解决下面的问题：已知$a+b=7,a^{2}b=50,ab^{2}=20$，求代数式$a^{3}+b^{3}$的值；
(3)小明同学用图3中x张边长为a的正方形纸片，y张边长为b的正方形纸片，z张宽、长分别为a，b的长方形纸片拼出一个面积为$(2a+b)(a+2b)$的长方形，求$x+y+z$的值；
【知识迁移】
(4)事实上，通过计算几何图形的体积也可以表示一些代数恒等式，图4表示的是一个棱长为x的正方体挖去一个小长方体后重新拼成一个新长方体，请你根据图4中图形的变化关系，写出一个代数恒等式：______。

答案： 解：
(1)$(a + b)^{3}=a^{3}+b^{3}+3a^{2}b + 3ab^{2}$
(2)因为 $a + b = 7$，$a^{2}b = 50$，$ab^{2}=20$，所以 $a^{3}+b^{3}=(a + b)^{3}-3a^{2}b - 3ab^{2}=343 - 3×50 - 3×20 = 133$.
(3)由题意，得 $(2a + b)(a + 2b)=xa^{2}+yb^{2}+zab$，所以 $2a^{2}+5ab + 2b^{2}=xa^{2}+yb^{2}+zab$，所以 $\begin{cases}x = 2,\\y = 2,\\z = 5,\end{cases}$ 所以 $x + y + z = 9$.
(4)$x^{3}-x=(x + 1)(x - 1)x$