2025年暑假总动员七年级数学沪科版合肥工业大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假总动员七年级数学沪科版合肥工业大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1. 如图,$AB// CD$,$∠E=40^{\circ}$,$∠A=110^{\circ}$,求$∠C$的度数.
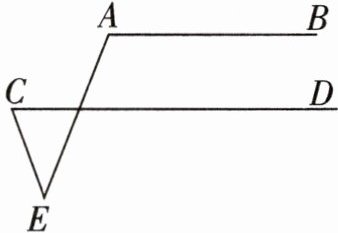

答案:
解:如图,过点E作EG//AB.因为AB//CD,EG//AB,所以CD//EG,所以∠GEA = 180° - ∠A = 70°,所以∠CEG = ∠CEA + ∠GEA = 110°,所以∠C = 180° - ∠CEG = 70°.

解:如图,过点E作EG//AB.因为AB//CD,EG//AB,所以CD//EG,所以∠GEA = 180° - ∠A = 70°,所以∠CEG = ∠CEA + ∠GEA = 110°,所以∠C = 180° - ∠CEG = 70°.

2. 直线$AB// CD$,$BE-EC$是一条折线段,$BP$平分$∠ABE$.
(1)如图1,若$BP// CE$,求证:$∠BEC+∠DCE=180^{\circ}$;
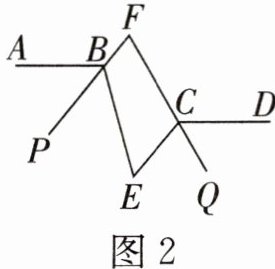
(2)$CQ$平分$∠DCE$,直线$BP$,$CQ$交于点$F$.
①如图2,写出$∠E$和$∠F$的数量关系,并证明;(注:三角形内角和为$180^{\circ}$)
②当点$E$在直线$AB$,$CD$之间时,若$∠E=40^{\circ}$,直接写出$∠F$的大小.
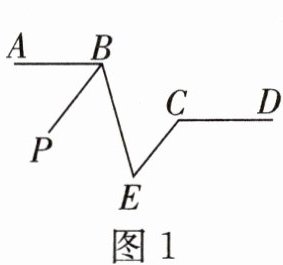
(1)如图1,若$BP// CE$,求证:$∠BEC+∠DCE=180^{\circ}$;
(2)$CQ$平分$∠DCE$,直线$BP$,$CQ$交于点$F$.
①如图2,写出$∠E$和$∠F$的数量关系,并证明;(注:三角形内角和为$180^{\circ}$)
②当点$E$在直线$AB$,$CD$之间时,若$∠E=40^{\circ}$,直接写出$∠F$的大小.


答案:
解:
(1)如图1,延长DC交BE于K,交BP于T,因为AB//CD,所以∠ABT = ∠BTK.因为BP平分∠ABE,所以∠ABT = ∠TBK,所以∠BTK = ∠TBK.因为BP//CE,所以∠BTK = ∠KCE,∠TBK = ∠KEC,所以∠KCE = ∠KEC.因为∠KCE + ∠DCE = 180°,所以∠KEC + ∠DCE = 180°,即∠BEC + ∠DCE = 180°.


(2)①∠E + 2∠F = 180°,证明如下:延长AB交FQ于M,延长DC交BE于N,如图2.因为射线BP,CQ分别平分∠ABE,∠DCE,所以∠ABP = ∠EBP,∠DCQ = ∠ECQ.设∠ABP = ∠EBP = α,∠DCQ = ∠ECQ = β,所以∠FBM = ∠ABP = α,∠MBE = 180° - 2α,∠NCE = 180° - 2β,∠FCN = ∠DCQ = β.因为AB//DC,所以∠FMB = ∠FCN = β,∠CNE = ∠MBE = 180° - 2α,所以∠F = 180° - ∠FBM - ∠FMB = 180° - (α + β),∠E = 180° - ∠NCE - ∠CNE = 180° - (180° - 2β) - (180° - 2α) = 2(α + β) - 180°,所以∠E = 180° - 2∠F,所以∠E + 2∠F = 180°.
②由①知,∠E + 2∠F = 180°,因为∠E = 40°,所以∠F = 70°.
解:
(1)如图1,延长DC交BE于K,交BP于T,因为AB//CD,所以∠ABT = ∠BTK.因为BP平分∠ABE,所以∠ABT = ∠TBK,所以∠BTK = ∠TBK.因为BP//CE,所以∠BTK = ∠KCE,∠TBK = ∠KEC,所以∠KCE = ∠KEC.因为∠KCE + ∠DCE = 180°,所以∠KEC + ∠DCE = 180°,即∠BEC + ∠DCE = 180°.


(2)①∠E + 2∠F = 180°,证明如下:延长AB交FQ于M,延长DC交BE于N,如图2.因为射线BP,CQ分别平分∠ABE,∠DCE,所以∠ABP = ∠EBP,∠DCQ = ∠ECQ.设∠ABP = ∠EBP = α,∠DCQ = ∠ECQ = β,所以∠FBM = ∠ABP = α,∠MBE = 180° - 2α,∠NCE = 180° - 2β,∠FCN = ∠DCQ = β.因为AB//DC,所以∠FMB = ∠FCN = β,∠CNE = ∠MBE = 180° - 2α,所以∠F = 180° - ∠FBM - ∠FMB = 180° - (α + β),∠E = 180° - ∠NCE - ∠CNE = 180° - (180° - 2β) - (180° - 2α) = 2(α + β) - 180°,所以∠E = 180° - 2∠F,所以∠E + 2∠F = 180°.
②由①知,∠E + 2∠F = 180°,因为∠E = 40°,所以∠F = 70°.
3. 如图,$AB// CD$,若$∠E+∠G=∠H$,试求$∠A+∠B+∠C+∠D+∠F$的度数.
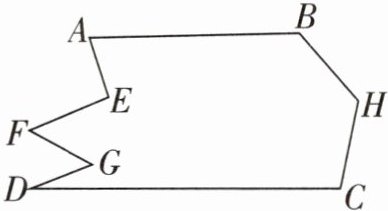

答案:
解:如图所示,作EI//AB,FJ//AB,GK//CD.因为AB//CD,所以AB//EI//FJ//GK//CD,所以∠A = ∠AEI,∠IEF = ∠EFJ,∠JFG = ∠FGK,∠KGD = ∠D,所以∠A + ∠EFG + ∠D = ∠AEF + ∠FGD = ∠H,所以∠A + ∠B + ∠C + ∠D + ∠F = ∠B + ∠C + ∠H = 360°.

解:如图所示,作EI//AB,FJ//AB,GK//CD.因为AB//CD,所以AB//EI//FJ//GK//CD,所以∠A = ∠AEI,∠IEF = ∠EFJ,∠JFG = ∠FGK,∠KGD = ∠D,所以∠A + ∠EFG + ∠D = ∠AEF + ∠FGD = ∠H,所以∠A + ∠B + ∠C + ∠D + ∠F = ∠B + ∠C + ∠H = 360°.

4. 已知,直线$AB// CD$,点$P$为平面上一点,连接$AP$与$CP$.
(1)如图1,点$P$在直线$AB$,$CD$之间,当$∠BAP=60^{\circ}$,$∠DCP=20^{\circ}$时,求$∠APC$的度数;
(2)如图2,点$P$在直线$AB$,$CD$之间,在$AC$左侧,$∠BAP$与$∠DCP$的角平分线相交于点$K$,写出$∠AKC$与$∠APC$之间的数量关系,并说明理由.
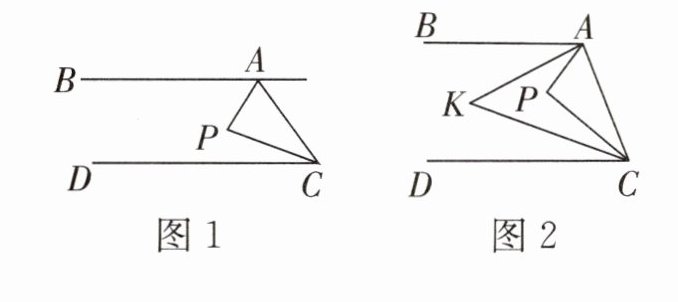
(1)如图1,点$P$在直线$AB$,$CD$之间,当$∠BAP=60^{\circ}$,$∠DCP=20^{\circ}$时,求$∠APC$的度数;
(2)如图2,点$P$在直线$AB$,$CD$之间,在$AC$左侧,$∠BAP$与$∠DCP$的角平分线相交于点$K$,写出$∠AKC$与$∠APC$之间的数量关系,并说明理由.

答案:
解:
(1)如图1,过P作PE//AB.因为AB//CD,所以PE//AB//CD,所以∠APC = ∠APE + ∠CPE = ∠BAP + ∠DCP = 60° + 20° = 80°.

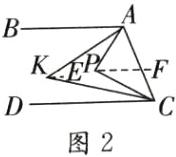
(2)∠AKC = $\frac{1}{2}$∠APC.理由:如图2,过K作KE//AB,因为AB//CD,所以KE//AB//CD,∠AKE = ∠BAK,∠CKE = ∠DCK,所以∠AKC = ∠AKE + ∠CKE = ∠BAK + ∠DCK.过P作PF//AB,同理可得,∠APC = ∠BAP + ∠DCP.因为∠BAP与∠DCP的角平分线交于点K,所以∠BAK + ∠DCK = $\frac{1}{2}$∠BAP + $\frac{1}{2}$∠DCP = $\frac{1}{2}$(∠BAP + ∠DCP) = $\frac{1}{2}$∠APC,所以∠AKC = $\frac{1}{2}$∠APC.
解:
(1)如图1,过P作PE//AB.因为AB//CD,所以PE//AB//CD,所以∠APC = ∠APE + ∠CPE = ∠BAP + ∠DCP = 60° + 20° = 80°.


(2)∠AKC = $\frac{1}{2}$∠APC.理由:如图2,过K作KE//AB,因为AB//CD,所以KE//AB//CD,∠AKE = ∠BAK,∠CKE = ∠DCK,所以∠AKC = ∠AKE + ∠CKE = ∠BAK + ∠DCK.过P作PF//AB,同理可得,∠APC = ∠BAP + ∠DCP.因为∠BAP与∠DCP的角平分线交于点K,所以∠BAK + ∠DCK = $\frac{1}{2}$∠BAP + $\frac{1}{2}$∠DCP = $\frac{1}{2}$(∠BAP + ∠DCP) = $\frac{1}{2}$∠APC,所以∠AKC = $\frac{1}{2}$∠APC.
查看更多完整答案,请扫码查看


