《2025年暑假总动员七年级数学沪科版合肥工业大学出版社》

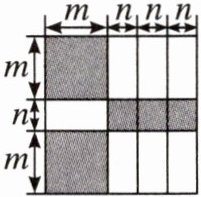
14. 如图,将一块长方形纸板裁剪成十二块,其中有两块是边长都为$m$的大正方形,三块是边长都为$n$的小正方形,七块是长为$m$,宽为$n$的完全相同的小长方形.观察图形,可以发现代数式$2m^{2}+7mn+3n^{2}$可以因式分解为____.

答案： $(2m+n)(m+3n)$ [解析]由题图可知,大长方形的两条邻边的长分别为$2m+n,m+3n$,所以大长方形纸板的面积为$(2m+n)(m+3n)$,又大长方形纸板的面积可以表示为$2m^{2}+7mn+3n^{2}$,所以$2m^{2}+7mn+3n^{2}=(2m+n)(m+3n).$

15. (8分)分解因式:
(1)$-2a^{3}+12a^{2}-18a$;
(2)$9a^{2}(x-y)+4b^{2}(y-x)$.

答案： 解:
(1)原式$=-2a(a^{2}-6a+9)=-2a(a-3)^{2}.$
(2)原式$=9a^{2}(x-y)-4b^{2}(x-y)=(x-y)\cdot (9a^{2}-4b^{2})=(x-y)(3a+2b)(3a-2b).$

16. (8分)计算:
(1)$[3a^{3}\cdot a^{3}+(-3a^{3})^{2}]÷(-2a^{2})^{3}$;
(2)$(-0.125)^{-2026}×(\frac {7}{4})^{2025}×(\frac {2024^{0}}{14})^{2024}$

答案： 解:
(1)原式$=(3a^{6}+9a^{6})÷(-8a^{6})=12a^{6}÷(-8a^{6})=-\frac {3}{2}.$
(2)原式$=(-8)^{2026}×(\frac {7}{4})^{2025}×(\frac {1}{14})^{2024}=(-8)^{2}×\frac {7}{4}×(-8×\frac {7}{4}×\frac {1}{14})^{2024}=112×(-1)^{2024}=112.$

17. (8分)先化简,再求值:$(a-2b)(a+2b)-(a-2b)^{2}+8b^{2}$,其中$a=-2$,$b=\frac {1}{2}$.

答案： 解:原式$=a^{2}-4b^{2}-a^{2}+4ab-4b^{2}+8b^{2}=4ab$.当$a=-2,b=\frac {1}{2}$时,原式$=-4.$

18. (8分)已知$a-b=1$且$ab=2$,求代数式$a^{3}b-2a^{2}b^{2}+ab^{3}$的值.

答案： 解:因为$a-b=1$且$ab=2$,所以$a^{3}b-2a^{2}b^{2}+ab^{3}=ab(a^{2}-2ab+b^{2})=ab(a-b)^{2}=2×1^{2}=2.$

19. (10分)在计算$(x+a)(x+b)$时,甲错把$b$看成了$6$,得到结果是$x^{2}+8x+12$;乙错把$a$看成了$-a$,得到结果是$x^{2}+x-6$.
(1)求出$a,b$的值;
(2)在(1)的条件下,计算$(x+a)(x+b)$的结果.

答案： 解:
(1)根据题意,得$(x+a)(x+6)=x^{2}+(6+a)x+6a=x^{2}+8x+12,(x-a)(x+b)=x^{2}+(-a+b)x-ab=x^{2}+x-6$,所以$6+a=8,-a+b=1$,解得$a=2,b=3.$
(2)当$a=2,b=3$时,$(x+a)(x+b)=(x+2)(x+3)=x^{2}+5x+6.$

20. (10分)仔细阅读下面例题并解答问题.
【例题】已知关于$x$的多项式$x^{2}-4x+m$有一个因式是$(x+3)$,求另一个因式及$m$的值.
解:设另一个因式为$(x+n)$,则$x^{2}-4x+m=(x+3)(x+n)$,即$x^{2}-4x+m=x^{2}+(n+3)x+3n$,所以$\left\{\begin{array}{l} n+3=-4,\\ 3n=m,\end{array}\right. $解得$\left\{\begin{array}{l} m=-21,\\ n=-7,\end{array}\right. $所以另一个因式为$(x-7)$,$m$的值为$-21$.
【问题】仿照以上方法解答下面问题:
(1)已知关于$x$的多项式$x^{2}+7x+a$有一个因式是$(x-2)$,求另一个因式及$a$的值;
(2)已知关于$x$的多项式$2x^{2}+3x-k$有一个因式是$(x+4)$,求$k$的值.

答案： 解:
(1)设另一个因式为$(x+m)$,则$x^{2}+7x+a=(x-2)(x+m)$,即$x^{2}+7x+a=x^{2}+(m-2)x-2m$,所以$\left\{\begin{array}{l} m-2=7,\\ -2m=a,\end{array}\right. $解得$\left\{\begin{array}{l} m=9,\\ a=-18,\end{array}\right. $所以另一个因式为$(x+9)$,a的值为-18.
(2)设另一个因式为$(2x+n)$,则$2x^{2}+3x-k=(x+4)(2x+n)$,即$2x^{2}+3x-k=2x^{2}+(n+8)x+4n$,所以$\left\{\begin{array}{l} n+8=3,\\ 4n=-k,\end{array}\right. $解得$\left\{\begin{array}{l} n=-5,\\ k=20,\end{array}\right. $所以k的值为20.