《2025年暑假总动员七年级数学沪科版合肥工业大学出版社》

6. 某商场购进商品后,加价40%作为销售价.五一期间,商场搞优惠促销,决定由顾客抽签确定折扣.某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款448元.两种商品原销售价之和为560元,则两种商品进价分别为______元和______元.

答案： 1. 设甲商品的进价为$x$元，乙商品的进价为$y$元：
因为加价$40\%$作为销售价，所以甲商品的销售价为$(1 + 40\%)x=1.4x$元，乙商品的销售价为$(1 + 40\%)y = 1.4y$元。
根据“两种商品原销售价之和为$560$元”，可列方程$1.4x+1.4y = 560$，化简得$x + y=\frac{560}{1.4}=400$，即$y = 400 - x$。
又因为顾客购买甲、乙两种商品，分别抽到七折和九折，共付款$448$元，所以$0.7×1.4x+0.9×1.4y = 448$。
2. 将$y = 400 - x$代入$0.7×1.4x+0.9×1.4y = 448$：
先对$0.7×1.4x+0.9×1.4y = 448$进行化简，根据乘法分配律$a(b + c)=ab+ac$，可得$1.4(0.7x + 0.9y)=448$，则$0.7x + 0.9y=\frac{448}{1.4}=320$。
把$y = 400 - x$代入$0.7x + 0.9y = 320$中，得到$0.7x+0.9(400 - x)=320$。
展开括号：$0.7x + 360-0.9x = 320$。
移项：$0.7x-0.9x=320 - 360$。
合并同类项：$-0.2x=-40$。
系数化为$1$：$x = 200$。
3. 求$y$的值：
把$x = 200$代入$y = 400 - x$，得$y = 400-200 = 200$。
所以两种商品进价分别为$200$元和$200$元。

7. 香江百货现推出水果篮和坚果礼盒,每个水果篮的成本为300元,每盒坚果礼盒的成本为250元;每个水果篮的售价比每盒坚果礼盒的售价多200元,售卖1个水果篮获得的利润和售卖2盒坚果礼盒获得的利润一样多.
(1)求每个水果篮和每盒坚果礼盒的售价;
(2)若香江百货第一批购进了200个水果篮和100盒坚果礼盒,为回馈客户香江百货计划将每个水果篮打折出售,坚果礼盒原价出售,售完这批水果篮和坚果礼盒共盈利15000元,按此计划每个水果篮应打几折出售?
(3)若香江百货花费5000元购进坚果礼盒后,当坚果礼盒售出$\frac{3}{5}$时,出现了滞销,于是决定降价促销,若要使坚果礼盒的销售利润为2600元,剩余的坚果礼盒每盒售价为多少元?

答案： $(1)$求每个水果篮和每盒坚果礼盒的售价
设每盒坚果礼盒的售价为$x$元，则每个水果篮的售价为$(x + 200)$元。
根据利润公式$利润=售价 - 成本$，已知售卖$1$个水果篮获得的利润和售卖$2$盒坚果礼盒获得的利润一样多，可列方程：
$(x + 200)-300 = 2×(x - 250)$
解这个方程：
$\begin{aligned}x + 200-300&=2x - 500\\x - 100&=2x - 500\\2x - x&=500 - 100\\x&=400\end{aligned}$
则水果篮售价为$x + 200=400 + 200 = 600$（元）。
所以，每个水果篮售价$600$元，每盒坚果礼盒售价$400$元。
$(2)$求每个水果篮应打几折出售
设每个水果篮打$y$折出售。
坚果礼盒的利润为$100×(400 - 250)=100×150 = 15000$（元）。
水果篮的售价为$600×0.1y$元，成本为$300$元，数量为$200$个，水果篮的利润为$200×(600×0.1y - 300)$元。
已知售完这批水果篮和坚果礼盒共盈利$15000$元，则可列方程：
$200×(600×0.1y - 300)+15000 = 15000$
$\begin{aligned}200×(60y - 300)+15000&=15000\\12000y-60000 + 15000&=15000\\12000y&=60000\\y&= 5\end{aligned}$
所以，每个水果篮应打$5$折出售。
$(3)$求剩余的坚果礼盒每盒售价为多少元
购进坚果礼盒的数量为$5000÷250 = 20$盒。
已售出$\frac{3}{5}×20 = 12$盒，已售出的利润为$12×(400 - 250)=12×150 = 1800$元。
设剩余的坚果礼盒每盒售价为$z$元，剩余数量为$20 - 12 = 8$盒，剩余的利润为$8×(z - 250)$元。
已知销售利润为$2600$元，则可列方程：
$1800+8×(z - 250)=2600$
$\begin{aligned}1800+8z-2000&=2600\\8z&=2600 + 200\\8z&=2800\\z&=350\end{aligned}$
所以，剩余的坚果礼盒每盒售价为$350$元。
综上，答案依次为：$(1)$水果篮售价$\boldsymbol{600}$元，坚果礼盒售价$\boldsymbol{400}$元；$(2)$$\boldsymbol{5}$折；$(3)$$\boldsymbol{350}$元。

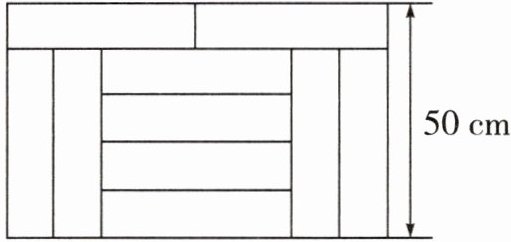
8. 如图,宽为50cm的长方形图案由10个形状大小完全相同的小长方形拼成,其中一个小长方形的面积为 ( )
A. 400cm² B. 500cm²
C. 600cm² D. 4000cm²

答案： 1. 设小长方形的长为$x cm$，宽为$y cm$：
根据图形可知：
由长方形的宽为$50cm$，可得$x + y=50$；
再根据小长方形的长与宽的关系（从图中可看出$x = 4y$）。
2. 解方程组$\begin{cases}x + y=50\\x = 4y\end{cases}$：
将$x = 4y$代入$x + y=50$中，得到$4y+y = 50$。
合并同类项：
根据合并同类项法则$ax+bx=(a + b)x$，这里$a = 4$，$b = 1$，则$4y+y=(4 + 1)y=5y$，所以$5y = 50$。
解得$y = 10$。
把$y = 10$代入$x = 4y$，得$x=4×10 = 40$。
3. 计算小长方形的面积$S$：
根据长方形面积公式$S=xy$。
把$x = 40$，$y = 10$代入公式，得$S=40×10=400(cm^{2})$。
所以一个小长方形的面积为$400cm^{2}$，答案是A。

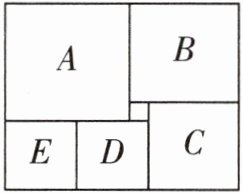
9. 如图所示,一个长方形恰好分成6个正方形,其中最小的正方形的边长是1,则这个长方形的面积是 ( )
A. 143 B. 168 C. 363 D. 572

答案： 1. 设正方形$D$的边长为$x$：
则正方形$C$的边长为$x$，正方形$E$的边长为$x$，正方形$B$的边长为$x + 1$，正方形$A$的边长为$x+2$。
2. 根据长方形的对边相等列方程：
由长方形的长相等可得：$(x + 2)+(x + 1)=x + x+x$。
化简方程$(x + 2)+(x + 1)=x + x+x$：
展开括号得$x + 2+x + 1=3x$。
移项得$3x-(x + x)=3$（根据等式性质$a=b$，则$a - c=b - c$，这里$c = 2x$）。
即$3x-2x = 3$，解得$x = 3$。
3. 求长方形的长和宽：
长方形的长：$(x + 2)+(x + 1)=(3 + 2)+(3 + 1)=9$。
长方形的宽：$(x + 2)+x=(3 + 2)+3 = 11$。
4. 求长方形的面积：
根据长方形面积公式$S=$长$×$宽，$S=9×13 = 143$。
所以这个长方形的面积是$143$，答案是A。

10. 我国明代数学读本《算法统宗》有一道题,其题意为客人一起分银子,若每人7两,还剩4两;若每人9两,则差8两.银子共有数目是 ( )
A. 44两 B. 45两 C. 46两 D. 47两

答案： 1. 设客人有$x$人：
根据银子总数不变列方程：
每人$7$两，还剩$4$两，则银子总数为$(7x + 4)$两；每人$9$两，则差$8$两，则银子总数为$(9x−8)$两。
所以$7x + 4=9x−8$。
2. 解方程：
移项，根据等式性质$1$：$ax + b=cx + d$（$a\neq c$），移项得$b - d=cx - ax$，即$4 + 8=9x−7x$。
合并同类项：$12 = 2x$。
系数化为$1$：根据等式性质$2$，$x=\frac{12}{2}=6$。
3. 求银子总数：
把$x = 6$代入$7x + 4$（也可代入$9x−8$）。
当$x = 6$时，$7x+4=7×6 + 4$。
先算乘法$7×6=42$，再算加法$42 + 4=46$（两）。
所以银子共有$46$两，答案是C。

11. 我国古代数学名著《张丘建算经》中记载:“今有清酒一斗直粟十斗,醑酒一斗直粟三斗,今持粟三斛,得酒五斗,问清、醑酒各几何?”意思是现在一斗清酒价值10斗谷子,一斗醑酒价值3斗谷子,现在拿29斗谷子,共换了5斗酒,问清、醑酒各几斗?

答案： 本题可通过设未知数，根据谷子总数和酒的总数列出方程组，进而求解清酒和醑酒的斗数。
步骤一：设未知数
设清酒$x$斗，醑酒$y$斗。
步骤二：根据已知条件列方程组
- **根据“共换了$5$斗酒”列方程：
清酒的斗数加上醑酒的斗数等于酒的总斗数，可列方程$x + y = 5$。
- **根据“拿$29$斗谷子”列方程：
已知一斗清酒价值$10$斗谷子，一斗醑酒价值$3$斗谷子，那么清酒的谷子数$10x$加上醑酒的谷子数$3y$等于谷子总数$29$，可列方程$10x + 3y = 29$。
因此，得到方程组$\begin{cases}x + y = 5\\10x + 3y = 29\end{cases}$。
步骤三：解方程组
由方程$x + y = 5$可得$y = 5 - x$，将其代入方程$10x + 3y = 29$中：
$\begin{aligned}10x + 3(5 - x)&= 29\\10x + 15 - 3x&= 29\\10x - 3x&= 29 - 15\\7x&= 14\\x&= 2\end{aligned}$
把$x = 2$代入$y = 5 - x$，可得$y = 5 - 2 = 3$。
综上，清酒$\boldsymbol{2}$斗，醑酒$\boldsymbol{3}$斗。