《2025年暑假总动员七年级数学沪科版合肥工业大学出版社》

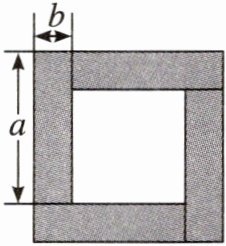
1. 如图，4块完全相同的长方形围成一个正方形，图中阴影部分的面积可以用不同的代数式进行表示，由此能验证的式子是()
A. $(a+b)(a-b)=a^{2}-b^{2}$
B. $(a+b)^{2}-(a-b)^{2}=2ab$
C. $(a+b)^{2}-(a-b)^{2}=4ab$
D. $(a-b)^{2}+2ab=a^{2}+b^{2}$

答案： C

2. 若干张面积分别为$a^{2},b^{2}$的正方形纸片和面积为$ab$的长方形纸片，小明从中抽取了1张面积为$b^{2}$的正方形纸片，6张面积为$ab$的长方形纸片。若他想拼成一个大正方形，则还需要抽取面积为$a^{2}$的正方形纸片()
A. 4张
B. 8张
C. 9张
D. 10张

答案： C

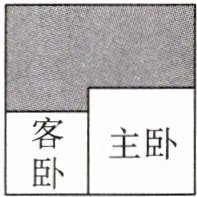
3. 如图为某正方形的房屋结构平面图，其中主卧与客卧都为正方形，其面积之和比其余面积(阴影部分)多$2.25m^{2}$，则主卧与客卧的周长差为()
A. 12m
B. 8m
C. 10m
D. 6m

答案： D[解析]设主卧的边长为 $a$ m，客卧边长为 $b$ m. 根据题意得，$(a^{2}+b^{2})-[(a + b)^{2}-(a^{2}+b^{2})]=2.25$，解得 $a - b = 1.5$，所以主卧与客卧的周长差为 $4(a - b)=6$.

4. 如图，点M是AB的中点，点P在MB上。分别以AP，PB为边，作正方形APCD和正方形PBEF，连接MD和ME。设$AP=a,BP=b$，且$a+b=10,ab=20$，则图中阴影部分的面积为______。

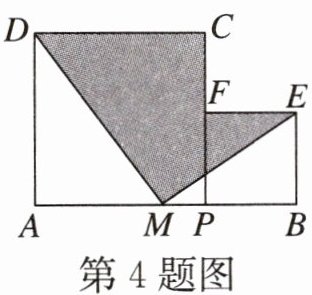
答案： 35

5. 如图，边长为6的正方形ABCD中放置两个长和宽分别为$a,b(a＜6,b＜6)$的长方形，若长方形的周长为16，面积为15.75，则图中阴影部分面积$S_{1}+S_{2}+S_{3}=$______。

答案： 12.5　[解析]由题图，得 $S_{1}=(6 - b)^{2}$，$S_{2}=(a + b - 6)^{2}$，$S_{3}=(6 - a)^{2}$，所以 $S_{1}+S_{2}+S_{3}=(6 - b)^{2}+(a + b - 6)^{2}+(6 - a)^{2}=2a^{2}+2b^{2}-24(a + b)+2ab + 108=2(a + b)^{2}-24(a + b)-2ab + 108$. 又 $2(a + b)=16$，$ab = 15.75$，所以 $a + b = 8$. 则 $S_{1}+S_{2}+S_{3}=2×8^{2}-24×8-2×15.75 + 108=12.5$.

6. 两个边长分别为a和b的正方形如图放置(图1)，其未叠合部分(阴影)面积为$S_{1}$；若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2)，两个小正方形叠合部分(阴影)面积为$S_{2}$。
(1)用含a，b的代数式分别表示$S_{1},S_{2}$；
(2)若$a-b=8,ab=13$，求$S_{1}+S_{2}$的值；
(3)用含a，b的代数式表示$S_{3}$；当$S_{1}+S_{2}=34$时，求出图3中阴影部分的面积$S_{3}$。

答案： 解：
(1)由题图可得，$S_{1}=a^{2}-b^{2}$，$S_{2}=b(2b - a)=2b^{2}-ab$.
(2)因为 $a - b = 8$，$ab = 13$，所以 $S_{1}+S_{2}=a^{2}-b^{2}+2b^{2}-ab=a^{2}+b^{2}-ab=(a - b)^{2}+ab=8^{2}+13=64 + 13=77$，所以 $S_{1}+S_{2}$ 的值为 77.
(3)由题图可得 $S_{3}=a^{2}+b^{2}-\frac{1}{2}b(a + b)-\frac{1}{2}a^{2}=\frac{1}{2}(a^{2}+b^{2}-ab)$. 因为 $S_{1}+S_{2}=a^{2}+b^{2}-ab = 34$，所以 $S_{3}=\frac{1}{2}×34 = 17$. 所以题图 3 中阴影部分的面积 $S_{3}$ 为 17.