2025年暑假总动员七年级数学沪科版合肥工业大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假总动员七年级数学沪科版合肥工业大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第63页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
1. 如图,超市里的购物车扶手AB与车底CD平行,∠2比∠3大10°,∠1是∠2的$1\frac{9}{11}$倍,则∠2的度数是( )
A. 55° B. 45° C. 44° D. 54°

A. 55° B. 45° C. 44° D. 54°

答案:
A [解析]设$∠2=x^{\circ }$,则$∠3=(x - 10)^{\circ }$,$∠1=\frac {20}{11}x^{\circ }$。因为$AB// CD$,所以$∠1=∠2 + ∠3$,所以$\frac {20}{11}x=x + x - 10$,解得$x = 55$,所以$∠2=55^{\circ }$。
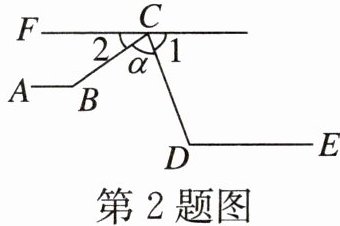
2. 如图,已知FC//AB//DE,∠α:∠D:∠B=2:3:4,则∠α的度数是______.

答案:
$72^{\circ }$ [解析]设$∠α=2x^{\circ }$,则$∠D=3x^{\circ }$,$∠B=4x^{\circ }$。因为$FC// AB// DE$,所以$∠2 + ∠B=180^{\circ }$,$∠1 + ∠D=180^{\circ }$,所以$∠2=180^{\circ } - ∠B=180^{\circ } - 4x^{\circ }$,$∠1=180^{\circ } - ∠D=180^{\circ } - 3x^{\circ }$。又因为$∠1 + ∠2 + ∠α=180^{\circ }$,所以$(180 - 3x)+(180 - 4x)+2x=180$,解得$x = 36$,所以$∠α=2x^{\circ }=72^{\circ }$。
3. 如图,AB//CD,EG平分∠DEF,FG平分∠BFE.
(1)求证:∠EFG+∠GEF=90°;
(2)在(1)的条件下,过点G作GH⊥AB,垂足为H,∠FGH的平分线GI交AB于点I,∠EGH的角平分线GJ交AB于点J,求∠IGJ的度数.

(1)求证:∠EFG+∠GEF=90°;
(2)在(1)的条件下,过点G作GH⊥AB,垂足为H,∠FGH的平分线GI交AB于点I,∠EGH的角平分线GJ交AB于点J,求∠IGJ的度数.

答案:
解:
(1)因为$AB// CD$,所以$∠DEF + ∠BFE=180^{\circ }$。因为$EG$平分$∠DEF$,$FG$平分$∠BFE$,所以$∠DEF=2∠GEF=2∠DEG$,$∠BFE=2∠EFG=2∠GFB$,所以$2∠GEF + 2∠EFG=180^{\circ }$,所以$∠EFG + ∠GEF=90^{\circ }$。
(2)如图,过点$G$作$GK// AB$。因为$AB// CD$,所以$AB// GK// CD$,所以$∠DEG=∠EGK$,$∠KGF=∠GFB$。由
(1)得,$∠DEG + ∠GFB=90^{\circ }$,所以$∠EGK + ∠KGF=90^{\circ }$。因为$GH⊥AB$,所以$GH⊥KG$,即$∠KGH=∠KGF + ∠HGF=90^{\circ }$,所以$∠EGK=∠HGF$。因为$GJ$平分$∠EGH$,所以$∠EGJ=∠HGJ$。又因为$∠KGJ=∠EGJ - ∠EGK$,$∠FGJ=∠HGJ - ∠HGF$,所以$∠KGJ=∠FGJ$,所以$∠KGF=2∠FGJ$。因为$GI$平分$∠HGF$,所以$∠HGF=2∠FGI$,所以$2∠FGJ + 2∠FGI=90^{\circ }$,即$∠FGJ + ∠FGI=45^{\circ }$,所以$∠IGJ=∠FGJ + ∠FGI=45^{\circ }$。

解:
(1)因为$AB// CD$,所以$∠DEF + ∠BFE=180^{\circ }$。因为$EG$平分$∠DEF$,$FG$平分$∠BFE$,所以$∠DEF=2∠GEF=2∠DEG$,$∠BFE=2∠EFG=2∠GFB$,所以$2∠GEF + 2∠EFG=180^{\circ }$,所以$∠EFG + ∠GEF=90^{\circ }$。
(2)如图,过点$G$作$GK// AB$。因为$AB// CD$,所以$AB// GK// CD$,所以$∠DEG=∠EGK$,$∠KGF=∠GFB$。由
(1)得,$∠DEG + ∠GFB=90^{\circ }$,所以$∠EGK + ∠KGF=90^{\circ }$。因为$GH⊥AB$,所以$GH⊥KG$,即$∠KGH=∠KGF + ∠HGF=90^{\circ }$,所以$∠EGK=∠HGF$。因为$GJ$平分$∠EGH$,所以$∠EGJ=∠HGJ$。又因为$∠KGJ=∠EGJ - ∠EGK$,$∠FGJ=∠HGJ - ∠HGF$,所以$∠KGJ=∠FGJ$,所以$∠KGF=2∠FGJ$。因为$GI$平分$∠HGF$,所以$∠HGF=2∠FGI$,所以$2∠FGJ + 2∠FGI=90^{\circ }$,即$∠FGJ + ∠FGI=45^{\circ }$,所以$∠IGJ=∠FGJ + ∠FGI=45^{\circ }$。

4. 阅读材料,完成问题.
三角形的内角和
小学时候我们就知道三角形的内角和是180°,学习了平行线之后,可以推导出三角形内角和是180°,方法如下:
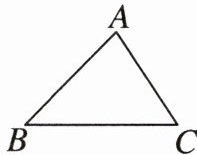
方法一:如图1,已知:三角形ABC,说明∠ABC+∠ACB+∠BAC=180°.
解:如图2,过点A作直线DE//BC,
因为DE//BC,
所以∠ABC=∠DAB,∠ACB=∠CAE.
因为∠DAB+∠BAC+∠CAE=180°,
所以∠ABC+∠ACB+∠BAC=180°,
即三角形的内角和是180°.
方法二:……
(1)方法一是用平行线的性质将三角形内角和问题转化为一个平角,这体现了数学中的______思想;
(2)请类比方法一,用平行线的性质,换一种方法推导出三角形内角和.

三角形的内角和
小学时候我们就知道三角形的内角和是180°,学习了平行线之后,可以推导出三角形内角和是180°,方法如下:
方法一:如图1,已知:三角形ABC,说明∠ABC+∠ACB+∠BAC=180°.
解:如图2,过点A作直线DE//BC,
因为DE//BC,
所以∠ABC=∠DAB,∠ACB=∠CAE.
因为∠DAB+∠BAC+∠CAE=180°,
所以∠ABC+∠ACB+∠BAC=180°,
即三角形的内角和是180°.
方法二:……
(1)方法一是用平行线的性质将三角形内角和问题转化为一个平角,这体现了数学中的______思想;
(2)请类比方法一,用平行线的性质,换一种方法推导出三角形内角和.


答案:
解:
(1)转化
(2)如图,延长$BC$至点$M$,过点$C$作$CN// AB$。因为$CN// AB$,所以$∠A=∠ACN$,$∠B=∠NCM$。因为$∠ACB + ∠ACN + ∠NCM=180^{\circ }$,所以$∠ABC + ∠ACB + ∠BAC=180^{\circ }$,即三角形的内角和是$180^{\circ }$。(答案不唯一)

解:
(1)转化
(2)如图,延长$BC$至点$M$,过点$C$作$CN// AB$。因为$CN// AB$,所以$∠A=∠ACN$,$∠B=∠NCM$。因为$∠ACB + ∠ACN + ∠NCM=180^{\circ }$,所以$∠ABC + ∠ACB + ∠BAC=180^{\circ }$,即三角形的内角和是$180^{\circ }$。(答案不唯一)

查看更多完整答案,请扫码查看


