2025年暑假总动员七年级数学沪科版合肥工业大学出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假总动员七年级数学沪科版合肥工业大学出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
14. $M$是个位数字不为零的两位数,将$M$的个位数字与十位数字互换后,得到另一个两位数$N$,若$M-N$恰是某正整数的立方,则这样的数共有____个.
答案:
6 [解析]设两位数$M=10a+b$,则$N=10b+a$,由题意得$a,b$为正整数,且$1\leqslant a\leqslant 9,1\leqslant b\leqslant 9$,所以$M-N=(10a+b)-(10b+a)=9(a-b)=c^{3}$.又$c$是某正整数,显然$c^{3}<100$,所以$c\leqslant 4$,而且$c^{3}$是9的倍数,所以$c=3$,即$a-b=3$,所以满足条件的两位数有41,52,63,74,85,96共6个.
15. (8分)已知:一个正数$a$的两个平方根分别是$x+3$和$2x-15$.
(1)求$x$的值;
(2)求$\frac{1}{7}a+1$的立方根.
(1)求$x$的值;
(2)求$\frac{1}{7}a+1$的立方根.
答案:
解:
(1)因为一个正数$a$的两个平方根分别是$x+3$和$2x-15$,所以$(x+3)+(2x-15)=0$,所以$3x-12=0$,解得$x=4.$
(2)由
(1)知$x=4$,则$x+3=7,2x-15=-7$,所以$a=7^{2}=49.\frac {1}{7}a+1=\frac {1}{7}×49+1=7+1=8$,所以$\frac {1}{7}a+1$的立方根是$\sqrt [3]{8}=2.$
(1)因为一个正数$a$的两个平方根分别是$x+3$和$2x-15$,所以$(x+3)+(2x-15)=0$,所以$3x-12=0$,解得$x=4.$
(2)由
(1)知$x=4$,则$x+3=7,2x-15=-7$,所以$a=7^{2}=49.\frac {1}{7}a+1=\frac {1}{7}×49+1=7+1=8$,所以$\frac {1}{7}a+1$的立方根是$\sqrt [3]{8}=2.$
16. (8分)求下列各式中$x$的值.
(1)$3(x-3)^2=27$;
(2)$(3x+1)^3+125=0$
(1)$3(x-3)^2=27$;
(2)$(3x+1)^3+125=0$
答案:
解:
(1)括号外系数化为1,得$(x-3)^{2}=9$.开平方,得$x-3=3$或$x-3=-3$,解得$x=6$或$x=0.$
(2)移项,得$(3x+1)^{3}=-125$.开立方,得$3x+1=-5$,移项,得$3x=-6$,系数化为1,得$x=-2.$
(1)括号外系数化为1,得$(x-3)^{2}=9$.开平方,得$x-3=3$或$x-3=-3$,解得$x=6$或$x=0.$
(2)移项,得$(3x+1)^{3}=-125$.开立方,得$3x+1=-5$,移项,得$3x=-6$,系数化为1,得$x=-2.$
17. (8分)如图,直径为$1$的圆从原点$O$沿数轴向左滚动一周,圆上与原点重合的点$O$到达点$O'$处,设点$O'$表示的数为$a$.
(1)求$a$的值;
(2)求$-(a-\sqrt{\frac{121}{25}})-\pi$的算术平方根.
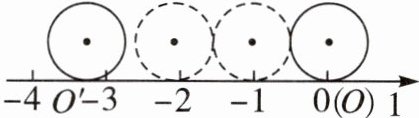
(1)求$a$的值;
(2)求$-(a-\sqrt{\frac{121}{25}})-\pi$的算术平方根.

答案:
解:
(1)由题意可知,$OO'$的长度等于直径为1的圆的周长,所以$OO'=π$.因为点$O'$在原点左侧,所以$a=-π$.故$a$的值为$-π$.
(2)把$a=-π$代入$-(a-\sqrt {\frac {121}{25}})-π$,得$-(-π-\sqrt {\frac {121}{25}})-π=\sqrt {\frac {121}{25}}=\frac {11}{5}$.因为$\frac {11}{5}$的算术平方根为$\sqrt {\frac {11}{5}}$,所以$-(a-\sqrt {\frac {121}{25}})-π$的算术平方根为$\sqrt {\frac {11}{5}}$.
(1)由题意可知,$OO'$的长度等于直径为1的圆的周长,所以$OO'=π$.因为点$O'$在原点左侧,所以$a=-π$.故$a$的值为$-π$.
(2)把$a=-π$代入$-(a-\sqrt {\frac {121}{25}})-π$,得$-(-π-\sqrt {\frac {121}{25}})-π=\sqrt {\frac {121}{25}}=\frac {11}{5}$.因为$\frac {11}{5}$的算术平方根为$\sqrt {\frac {11}{5}}$,所以$-(a-\sqrt {\frac {121}{25}})-π$的算术平方根为$\sqrt {\frac {11}{5}}$.
18. (8分)观察下面的运算过程:
计算:$1+2+2^2+\cdots+2^{10}$.
解:设$S=1+2+2^2+\cdots+2^{10}\cdots$①,
①$× 2$,得$2S=2+2^2+2^3+\cdots+2^{11}\cdots$②,
②$-$①,得$S=2^{11}-1$,
所以$1+2+2^2+\cdots+2^{10}=2^{11}-1$.
运用上面的计算方法计算:
$1+3+3^2+\cdots+3^{2026}$.
计算:$1+2+2^2+\cdots+2^{10}$.
解:设$S=1+2+2^2+\cdots+2^{10}\cdots$①,
①$× 2$,得$2S=2+2^2+2^3+\cdots+2^{11}\cdots$②,
②$-$①,得$S=2^{11}-1$,
所以$1+2+2^2+\cdots+2^{10}=2^{11}-1$.
运用上面的计算方法计算:
$1+3+3^2+\cdots+3^{2026}$.
答案:
解:设$S=1+3+3^{2}+3^{3}+... +3^{2026}$…①,①×3,得$3S=3+3^{2}+3^{3}+... +3^{2027}$…②,②-①,得$2S=3^{2027}-1$,所以$S=\frac {3^{2027}-1}{2}$,所以$1+3+3^{2}+3^{3}+... +3^{2026}=\frac {3^{2027}-1}{2}.$
19. (10分)如图,这是由$8$个同样大小的正方体组成的魔方,体积为$8\mathrm{cm}^3$.
(1)求这个魔方的棱长;
(2)图中阴影部分是一个正方形,求出阴影部分的周长.

(1)求这个魔方的棱长;
(2)图中阴影部分是一个正方形,求出阴影部分的周长.

答案:
解:
(1)因为$\sqrt [3]{8}=2$,所以这个魔方的棱长是2 cm.
(2)因为魔方的棱长为2 cm,所以其中任意一个面的面积为$4cm^{2}$,所以阴影部分这个正方形的面积为一个面的面积的一半,为$2cm^{2}$,其边长为$\sqrt {2}cm$,所以阴影部分的周长为$4\sqrt {2}cm$.
(1)因为$\sqrt [3]{8}=2$,所以这个魔方的棱长是2 cm.
(2)因为魔方的棱长为2 cm,所以其中任意一个面的面积为$4cm^{2}$,所以阴影部分这个正方形的面积为一个面的面积的一半,为$2cm^{2}$,其边长为$\sqrt {2}cm$,所以阴影部分的周长为$4\sqrt {2}cm$.
查看更多完整答案,请扫码查看


