2025年实验班提优训练暑假衔接版八升九年级数学浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练暑假衔接版八升九年级数学浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
23. 为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了如下统计图表:
甲、乙射击成绩统计表
| | 平均数 | 中位数 | 方差 | 命中10环的次数 |
| --- | --- | --- | --- | --- |
| 甲 | 7 | | | 0 |
| 乙 | | | | 1 |
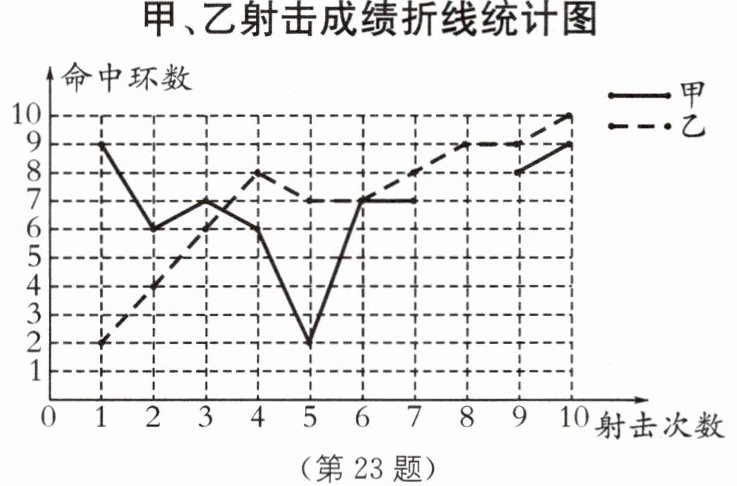
(1)请补全上述图表.(请直接在表中填空和补全折线图)
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由.
甲、乙射击成绩统计表
| | 平均数 | 中位数 | 方差 | 命中10环的次数 |
| --- | --- | --- | --- | --- |
| 甲 | 7 | | | 0 |
| 乙 | | | | 1 |

(1)请补全上述图表.(请直接在表中填空和补全折线图)
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由.
答案:
(1)略
(2)由乙的方差大于甲的方差,得到甲胜出
(1)略
(2)由乙的方差大于甲的方差,得到甲胜出
24. 如图,正比例函数$y = \frac{1}{2}x$的图象与反比例函数$y = \frac{k}{x}(k \neq 0)$在第一象限的图象交于点$A$,过点$A$作$x$轴的垂线,垂足为$M$,已知$\triangle OAM$的面积为1.
(1)求反比例函数的表达式;
(2)如果$B$为反比例函数在第一象限图象上的点(点$B$与点$A$不重合),且点$B$的横坐标为1,在$x$轴上求一点$P$,使$PA + PB$最小.
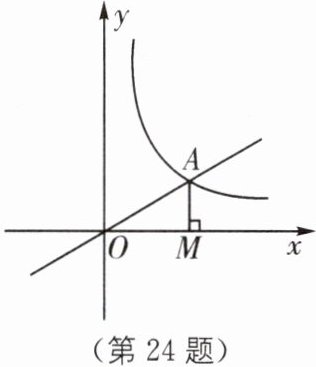
(1)求反比例函数的表达式;
(2)如果$B$为反比例函数在第一象限图象上的点(点$B$与点$A$不重合),且点$B$的横坐标为1,在$x$轴上求一点$P$,使$PA + PB$最小.

答案:
(1)y=$\frac{2}{x}$
(2)联立$\begin{cases}y=\frac{2}{x},\\y=\frac{1}{2}x,\end{cases}$解得$\begin{cases}x = -2,\\y = -1\end{cases}$或$\begin{cases}x = 2,\\y = 1.\end{cases}$
∴点A的坐标为(2,1).
设点A关于x轴的对称点为C,则点C的坐标为(2,−1).若要在x轴上求一点P,使PA+PB最小,即PB+PC最小,则点P应为BC与x轴的交点,如图

设直线BC的表达式为y=mx+n.
由题意,得点B的坐标为(1,2),
∴$\begin{cases}2 = m + n,\\-1 = 2m + n,\end{cases}$解得$\begin{cases}m = -3,\\n = 5.\end{cases}$
∴直线BC的表达式为y=−3x+5.
当y=0时,x=$\frac{5}{3}$.
∴点P的坐标为($\frac{5}{3}$,0).
(1)y=$\frac{2}{x}$
(2)联立$\begin{cases}y=\frac{2}{x},\\y=\frac{1}{2}x,\end{cases}$解得$\begin{cases}x = -2,\\y = -1\end{cases}$或$\begin{cases}x = 2,\\y = 1.\end{cases}$
∴点A的坐标为(2,1).
设点A关于x轴的对称点为C,则点C的坐标为(2,−1).若要在x轴上求一点P,使PA+PB最小,即PB+PC最小,则点P应为BC与x轴的交点,如图

设直线BC的表达式为y=mx+n.
由题意,得点B的坐标为(1,2),
∴$\begin{cases}2 = m + n,\\-1 = 2m + n,\end{cases}$解得$\begin{cases}m = -3,\\n = 5.\end{cases}$
∴直线BC的表达式为y=−3x+5.
当y=0时,x=$\frac{5}{3}$.
∴点P的坐标为($\frac{5}{3}$,0).
查看更多完整答案,请扫码查看


