《2025年实验班提优训练暑假衔接版八升九年级数学浙教版》

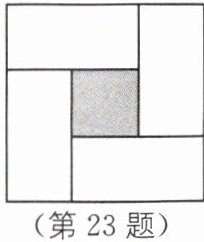
23. 传统文化 《周髀算经》 《周髀算经》中有一种几何方法可以用来解形如 $ x(x + 5)=24 $ 的方程的正数解，方法为：如图，将四个长为 $ x + 5 $，宽为 $ x $ 的长方形纸片（面积均为 $ 24 $）拼成一个大正方形，于是大正方形的面积为 $ 24\times4 + 25 = 121 $，边长为 $ 11 $，故得 $ x(x + 5)=24 $ 的正数解为 $ x=\frac{11 - 5}{2}=3 $. 小明按此方法解关于 $ x $ 的方程 $ x^{2}+mx - n = 0 $ 时，构造出同样的图形. 已知大正方形的面积为 $ 12 $，小正方形的面积为 $ 4 $，求方程的正数解.

答案：
∵x²+mx−n=0,
∴x(x+m)=n,
∴图中长方形的长为(x+m),宽为x，
∴图中小正方形的边长为x+m−x=m=√4=2,大正方形的边长为x+m+x=2x+m=$\sqrt{12}$,
∴x=$\frac{\sqrt{12}−2}{2}$=√3−1.

24. 新情境 推广节水型灌溉技术 随着农业技术的现代化，节水型灌溉得到逐步推广. 喷灌和滴灌是比漫灌更节水的灌溉方式，喷灌和滴灌时每亩用水量分别是漫灌时的 $ 30\% $ 和 $ 20\% $. 去年，某丰收公司用各 $ 100 $ 亩的三块试验田分别采用喷灌、滴灌和漫灌的灌溉方式，共用水 $ 15000 $ 吨.
（1）请问用漫灌方式每亩用水多少吨？去年每块试验田各用水多少吨？
（2）今年该公司加大对农业灌溉的投入，喷灌和滴灌试验田的面积都增加了 $ m\% $，漫灌试验田的面积减少了 $ 2m\% $. 同时，该公司通过维修灌溉输水管道，使得三种灌溉方式下的每亩用水量都进一步减少了 $ m\% $. 经测算，今年的灌溉用水量比去年减少 $ \frac{9}{5}m\% $，求 $ m $ 的值.
（3）节水不仅为了环保，也与经济收益有关系. 今年，该公司全部试验田在灌溉输水管道维修方面每亩投入 $ 30 $ 元，在新增的喷灌、滴灌试验田添加设备所投入经费为每亩 $ 100 $ 元，在（2）的情况下，若每吨水费为 $ 2.5 $ 元，请判断，相比去年因用水量减少所节省的水费是否大于今年以上两项的投入之和？

答案：
(1)设漫灌方式每亩用水x吨，
　则100x+100×30%x+100×20%x=15000,
　解得x=100,
∴漫灌用水:100×100=10000(吨),
　喷灌用水:30%×10000=3000(吨),
　滴灌用水:20%×10000=2000(吨),
∴漫灌方式每亩用水100吨，漫灌试验田用水10000吨，喷灌试验田用水3000吨，滴灌试验田用水2000吨
(2)由题意,得100×(1−2m%)×100×(1−m%)
　+100×(1+m%)×30×(1−m%)+100×(1+m%)×20×(1−m%)=15000×(1−$\frac{9}{5}$m%),
　解得m=0(舍去)或m=20,
∴m=20.
(3)节省水费:15000×$\frac{9}{5}$m%×2.5=13500(元),维修投入:300×30=9000(元),
新增设备:100×2m%×100=4000(元),
又13500＞9000+4000,
∴节省水费大于两项投入之和.