《2025年实验班提优训练暑假衔接版八升九年级数学浙教版》

10. 甲、乙两人在直线跑道上同起点、同终点、同方向匀速跑步500m，先到终点的人原地休息. 已知甲先出发2s，在跑步过程中，甲、乙两人之间的距离$y(m)$与乙的出发的时间$t(s)$之间的关系如图所示，给出以下结论：①$a=8$；②$b=92$；③$c=123$. 其中正确的是（ ）.

A. ①②③
B. 仅有①②
C. 仅有①③
D. 仅有②③

答案： A

11. 将一副三角尺按如图所示放置，则$∠1=$______$^{\circ}$.

答案： 105

12. 在平面直角坐标系中，点$P(m,m-2)$在第一象限内，则$m$的取值范围是______.

答案： $ m ＞ 2 $

13. 下列命题中，其逆命题成立的是______.（填写序号）
①同旁内角互补，两直线平行；
②如果两个角是直角，那么它们相等；
③如果两个实数相等，那么它们的平方相等；
④如果三角形的三边长$a,b,c$满足$a^{2}+b^{2}=c^{2}$，那么这个三角形是直角三角形.

答案： ①④

14. 中考新考法 满足结论的条件开放 如图，$BC=EC$，$∠1=∠2$，要使$\triangle ABC≌\triangle DEC$，则应添加的一个条件为______.（答案不唯一，只需填一个）

答案： $ AC = DC $（答案不唯一）

15. 如图，在平面直角坐标系中，$\triangle ABC$经过平移后点$A$的对应点为点$A'$，则平移后点$B$的对应点$B'$的坐标为______.

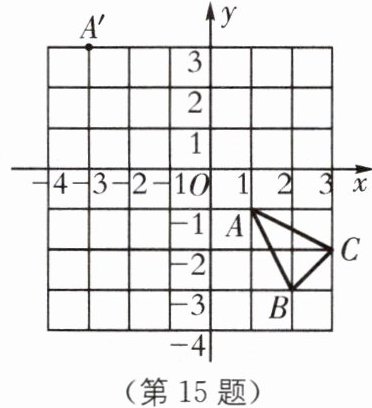
答案： $ (-2,1) $

16. 若一次函数$y=(2m-1)x+3-2m$的图象经过第一、二、四象限，则$m$的取值范围是______.

答案： $ m ＜ \frac{1}{2} $

17. 若$a,b,c,d$为整数，且$a＜3b,b＜5c,c＜7d,d＜30$，则$a$的最大值为______.

答案： 3026

18. 如图，在$\triangle ABC$中，$∠ACB=90^{\circ}$，点$D$是$BC$的中点，$DE⊥BC,CE// AD$，若$AC=2,CE=4$，则四边形$ACEB$的周长为______.

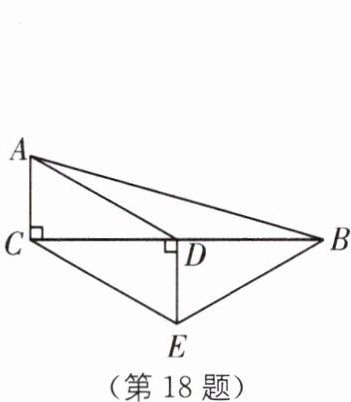
答案： $ 10 + 2\sqrt{13} $

19. 解下列不等式（组），并把解集表示在数轴上.
（1）$\frac{2+x}{4}\geq\frac{2x-1}{3}$；
（2）$\begin{cases}2x+7＞3x-1,\\\frac{x-2}{5}\geq0.\end{cases}$

答案： 图略
(1) $ x \leq 2 $
(2) $ 2 \leq x ＜ 8 $

20. 如图，已知点$D$为等腰直角三角形$ABC$内一点，$∠CAD=∠CBD=15^{\circ}$，$E$为$AD$延长线上的一点，且$CE=CA$.
（1）求证：$DE$平分$∠BDC$；
（2）若点$M$在$DE$上，且$DC=DM$，求证：$ME=BD$.

答案：
(1) 在等腰直角三角形 $ ABC $ 中，$ AC = BC $，$ \angle CAB = \angle CBA = 45^{\circ} $，
$ \because \angle CAD = \angle CBD = 15^{\circ} $。
$ \therefore \angle BAD = \angle ABD = 45^{\circ} - 15^{\circ} = 30^{\circ} $。
$ \therefore BD = AD $。$ \therefore \triangle BDC \cong \triangle ADC $。
$ \therefore \angle DCA = \angle DCB = 45^{\circ} $。
$ \because \angle BDM = \angle ABD + \angle BAD = 30^{\circ} + 30^{\circ} = 60^{\circ} $，$ \angle EDC = \angle DAC + \angle DCA = 15^{\circ} + 45^{\circ} = 60^{\circ} $，
$ \therefore \angle BDM = \angle EDC $。$ \therefore DE $ 平分 $ \angle BDC $。
(2) 连结 $ MC $。
$ \because DC = DM $，且 $ \angle MDC = 60^{\circ} $，
$ \therefore \triangle MDC $ 是等边三角形。
$ \therefore CM = CD $，$ \angle DMC = 60^{\circ} $。
又 $ \angle EMC = 180^{\circ} - \angle DMC = 180^{\circ} - 60^{\circ} = 120^{\circ} $，$ \angle ADC = 180^{\circ} - \angle MDC = 180^{\circ} - 60^{\circ} = 120^{\circ} $，
$ \therefore \angle EMC = \angle ADC $。
又 $ CE = CA $，$ \therefore \angle DAC = \angle CEM = 15^{\circ} $。
$ \therefore \triangle ADC \cong \triangle EMC $。$ \therefore ME = AD = BD $。