2025年实验班提优训练暑假衔接版八升九年级数学浙教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练暑假衔接版八升九年级数学浙教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
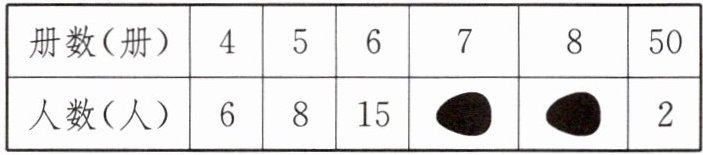
21. 某校九(1)班积极响应校团委的号召,每位同学都向“希望工程”捐献图书,全班$40$名同学共捐图书$320$册.特别值得一提的是小扬、小州两位同学在父母的支持下各捐献了$50$册图书.班长统计了全班捐书情况如表(被粗心的小虎用墨水污染了一部分):
|册数(册)|$4$|$5$|$6$|$7$|$8$|$50$|
|----|----|----|----|----|----|----|
|人数(人)|$6$|$8$|$15$|||$2$|
分别求出该班级捐献$7$册图书和$8$册图书的人数.
|册数(册)|$4$|$5$|$6$|$7$|$8$|$50$|
|----|----|----|----|----|----|----|
|人数(人)|$6$|$8$|$15$|||$2$|
分别求出该班级捐献$7$册图书和$8$册图书的人数.

答案:
捐献7册的人数为6人,捐献8册的人数为3人
22. 已知一组数据$x_1$,$x_2$,$\cdots$,$x_6$的平均数为$2$,方差为$2$.
(1)求$x_1^2 + x_2^2 + \cdots + x_6^2$;
(2)若在这组数据中加入另一个数据$x_7$,重新计算,平均数无变化,求这$7$个数据的方差(结果用分数表示).
(1)求$x_1^2 + x_2^2 + \cdots + x_6^2$;
(2)若在这组数据中加入另一个数据$x_7$,重新计算,平均数无变化,求这$7$个数据的方差(结果用分数表示).
答案:
(1)
∵数据x1,x2,...,x6的平均数为2,
∴x1+x2+...+x6=2×6=12.
又方差为2,
∴S²=$\frac{1}{6}$[(x1−2)²+(x2−2)²+...+(x6−2)²]=$\frac{1}{6}$[x1²+x2²+…+x6²−4(x1+x2+…+x6)+24]=$\frac{1}{6}$(x1²+x2²+...+x6²−4×12+24)=$\frac{1}{6}$(x1²+x2²+...+x6²−24)=2,
∴x1²+x2²+...+x6²=36.
(2)
∵数据x1,x2,...,x7的平均数为2,
∴x1+x2+...+x7=2×7=14,
∵x1+x2+...+x6=12,
∴x7=2.
∵$\frac{1}{6}$[(x1−2)²+(x2−2)²+...+(x6−2)²]=2,
∴(x1−2)²+(x2−2)²+...+(x6−2)²=12.
∴S²=$\frac{1}{7}$[(x1−2)²+(x2−2)²+...+(x7−2)²]=$\frac{1}{7}$[12+(2−2)²]=$\frac{12}{7}$.
(1)
∵数据x1,x2,...,x6的平均数为2,
∴x1+x2+...+x6=2×6=12.
又方差为2,
∴S²=$\frac{1}{6}$[(x1−2)²+(x2−2)²+...+(x6−2)²]=$\frac{1}{6}$[x1²+x2²+…+x6²−4(x1+x2+…+x6)+24]=$\frac{1}{6}$(x1²+x2²+...+x6²−4×12+24)=$\frac{1}{6}$(x1²+x2²+...+x6²−24)=2,
∴x1²+x2²+...+x6²=36.
(2)
∵数据x1,x2,...,x7的平均数为2,
∴x1+x2+...+x7=2×7=14,
∵x1+x2+...+x6=12,
∴x7=2.
∵$\frac{1}{6}$[(x1−2)²+(x2−2)²+...+(x6−2)²]=2,
∴(x1−2)²+(x2−2)²+...+(x6−2)²=12.
∴S²=$\frac{1}{7}$[(x1−2)²+(x2−2)²+...+(x7−2)²]=$\frac{1}{7}$[12+(2−2)²]=$\frac{12}{7}$.
23. 某初中数学老师要从甲、乙两位学生中选一名参加数学竞赛,甲、乙两人前五学期的数学成绩如表:
| |第一学期|第二学期|第三学期|第四学期|第五学期|
|----|----|----|----|----|----|
|甲|$75$|$80$|$85$|$90$|$95$|
|乙|$95$|$87$|$88$|$80$|$75$|
(1)分别求出甲、乙两人前五学期的数学平均成绩.
(2)分别画出甲、乙前五学期的数学成绩折线统计图.
(3)如果你是老师,你认为该选哪位学生参加数学竞赛?请简要说明理由.
| |第一学期|第二学期|第三学期|第四学期|第五学期|
|----|----|----|----|----|----|
|甲|$75$|$80$|$85$|$90$|$95$|
|乙|$95$|$87$|$88$|$80$|$75$|
(1)分别求出甲、乙两人前五学期的数学平均成绩.
(2)分别画出甲、乙前五学期的数学成绩折线统计图.
(3)如果你是老师,你认为该选哪位学生参加数学竞赛?请简要说明理由.
答案:
(1)甲的前五学期的数学平均成绩为85;乙的前五学期的数学平均成绩为85.
(2)图略
(3)无论从数据变化来看,还是从折线图来看,甲同学的成绩逐步上升的趋势非常明显,且成绩能达到95分的水平,而乙同学的成绩呈逐步下滑的趋势,故选派甲同学参加竞赛是非常合适的.
(1)甲的前五学期的数学平均成绩为85;乙的前五学期的数学平均成绩为85.
(2)图略
(3)无论从数据变化来看,还是从折线图来看,甲同学的成绩逐步上升的趋势非常明显,且成绩能达到95分的水平,而乙同学的成绩呈逐步下滑的趋势,故选派甲同学参加竞赛是非常合适的.
查看更多完整答案,请扫码查看


