《2025年实验班提优训练暑假衔接版八升九年级数学浙教版》

23. 中考新考法 解题方法型阅读理解题 阅读下面的解答过程，然后作答：
有这样一类题目：将$\sqrt {a+2\sqrt {b}}$化简，若你能找到两个数$m$和$n$，使$m^{2}+n^{2}=a$且$mn=\sqrt {b}$，则$a+2\sqrt {b}$可变为$m^{2}+n^{2}+2mn$，即变成$(m+n)^{2}$，从而使得$\sqrt {a+2\sqrt {b}}=m+n$。
化简：
例如：$\because 5+2\sqrt {6}=3+2+2\sqrt {6}=(\sqrt {3})^{2}+(\sqrt {2})^{2}+2\sqrt {6}=(\sqrt {3}+\sqrt {2})^{2}$，
$\therefore \sqrt {5+2\sqrt {6}}=\sqrt {(\sqrt {3}+\sqrt {2})^{2}}=\sqrt {3}+\sqrt {2}$。
请你仿照上例将下列各式化简：
(1)$\sqrt {4+2\sqrt {3}}$；
(2)$\sqrt {7-2\sqrt {10}}$。

答案：
(1)
∵4+2$\sqrt{3}$=1+3+2$\sqrt{3}$=1²+($\sqrt{3}$)²+2$\sqrt{3}$=(1 +$\sqrt{3}$)²,
∴$\sqrt{4+2\sqrt{3}}=\sqrt{(1+\sqrt{3})²}=1+\sqrt{3}$.
(2)
∵7−2$\sqrt{10}$=($\sqrt{5}$)²+($\sqrt{2}$)²−2×$\sqrt{5}$×$\sqrt{2}$=($\sqrt{5}-\sqrt{2}$)²,
∴$\sqrt{7-2\sqrt{10}}=\sqrt{(\sqrt{5}-\sqrt{2})²}=\sqrt{5}-\sqrt{2}$.

24. 在进行二次根式化简时，我们有时会碰上如$\frac {3}{\sqrt {5}},\sqrt {\frac {2}{3}},\frac {2}{\sqrt {3}+1}$一样的式子，其实我们还可以将其进一步化简：
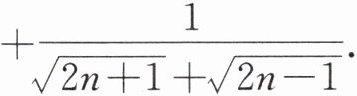
$\frac {3}{\sqrt {5}}=\frac {3×\sqrt {5}}{\sqrt {5}×\sqrt {5}}=\frac {3\sqrt {5}}{5}$；(一)
$\sqrt {\frac {2}{3}}=\sqrt {\frac {2×3}{3×3}}=\frac {\sqrt {6}}{3}$；(二)
$\frac {2}{\sqrt {3}+1}=\frac {2×(\sqrt {3}-1)}{(\sqrt {3}+1)(\sqrt {3}-1)}=\frac {2(\sqrt {3}-1)}{(\sqrt {3})^{2}-1^{2}}=\sqrt {3}-1$。(三)
以上这种化简的步骤叫做分母有理化。
$\frac {2}{\sqrt {3}+1}$还可以用以下方法化简：
$\frac {2}{\sqrt {3}+1}=\frac {3-1}{\sqrt {3}+1}=\frac {(\sqrt {3})^{2}-1^{2}}{\sqrt {3}+1}=\frac {(\sqrt {3}+1)(\sqrt {3}-1)}{\sqrt {3}+1}=\sqrt {3}-1$。(四)
(1)请用不同的方法化简：$\frac {2}{\sqrt {5}+\sqrt {3}}$。
①参照(三)式，得$\frac {2}{\sqrt {5}+\sqrt {3}}=$____；
②参照(四)式，得$\frac {2}{\sqrt {5}+\sqrt {3}}=$____。
(2)化简：$\frac {1}{\sqrt {3}+1}+\frac {1}{\sqrt {5}+\sqrt {3}}+\frac {1}{\sqrt {7}+\sqrt {5}}+…+\frac {1}{\sqrt {2n+1}+\sqrt {2n-1}}$。

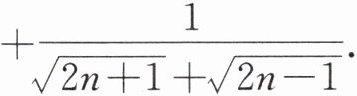
答案：
(1)①$\frac{2×(\sqrt{5}-\sqrt{3})}{(\sqrt{5})^{2}-(\sqrt{3})^{2}}=\frac{2(\sqrt{5}-\sqrt{3})}{5 - 3}=\sqrt{5}-\sqrt{3}$；②$\frac{(\sqrt{5})^{2}-(\sqrt{3})^{2}}{\sqrt{5}+\sqrt{3}}=\frac{(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})}{\sqrt{5}+\sqrt{3}}=\sqrt{5}-\sqrt{3}$
(2)原式=$\frac{1}{2}$×($\sqrt{3}-1+\sqrt{5}-\sqrt{3}+\sqrt{7}-\sqrt{5}+...+\sqrt{2n+1}-\sqrt{2n-1}$)=$\frac{\sqrt{2n+1}-1}{2}$.