《2025年实验班提优训练暑假衔接版八升九年级数学浙教版》

19. 已知函数 $ y = ( 5 m - 3 ) x ^ { 2 - n } + ( m + n ) $.
（1）当 $ m $，$ n $ 为何值时，它是一次函数？
（2）当 $ m $，$ n $ 为何值时，它是正比例函数？
（3）当 $ m $，$ n $ 为何值时，它是反比例函数？

答案：
(1)当函数y=(5m−3)x²−+(m+n)是一次函数时,2−n=1,且5m−3≠0,解得n=1,m≠35​.
(2)当函数y=(5m−3)x²−+(m+n)是正比例函
　　数时，2−n=1,
                  {m+n=0,解得n=1,m=−1.
　　　　    5m−3≠0,
(3)当函数y=(5m−3)x²−+(m+n)是反比例函
　数时,2−n=−1,
           m+n=0,解得n=3,m=−3.
　　    5m−3≠0,

20. 已知一次函数 $ y = - x + 4 $ 和反比例函数 $ y = \frac { k } { x } ( k \neq 0 ) $.
（1）当 $ k $ 满足什么条件时这两个函数的图象有两个交点？
（2）设这两个函数图象的公共点为 $ A $，$ B $，当 $ \angle A O B $ 分别是锐角和钝角时，写出 $ k $ 的取值范围.

答案：
(1)k＜4且k≠0
(2)当∠AOB是锐角时,0＜k＜4;当∠AOB是钝角时，k＜0.

21. 跨学科 杠杆原理 小明想要用撬棍撬动一块大石头，已知阻力为 $ 1 600 \mathrm { N } $，阻力臂长为 $ 0.5 \mathrm { m } $. 设动力为 $ y ( \mathrm { N } ) $，动力臂长为 $ x ( \mathrm { m } ) $.（杠杆平衡时，动力 $ \times $ 动力臂 $ = $ 阻力 $ \times $ 阻力臂，其中撬棍本身所受的重力略去不计）
（1）求 $ y $ 关于 $ x $ 的函数表达式（不要求写自变量的取值范围）.
（2）当动力臂长为 $ 2 \mathrm { m } $ 时，撬动石头至少需要多大的力？

答案：
(1)由题意，得xy=1600×0.5,则y=$\frac{800}{x}$.
　故y关于x的函数表达式为y=$\frac{800}{x}$.
(2)
∵y=$\frac{800}{x}$,
∴当x=2时,y=$\frac{800}{2}$=400.故当动力臂长为2m时，撬动石头至少需要400N的力.

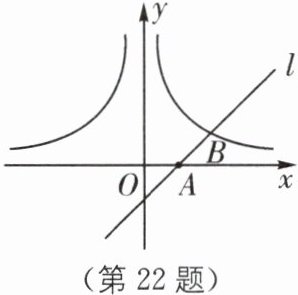
22. 如图，直线 $ l $ 经过点 $ A ( 1, 0 ) $，且与双曲线 $ y = \frac { m } { x } ( x ＞ 0 ) $ 交于点 $ B ( 2, 1 ) $，过点 $ P ( p, p - 1 ) ( p ＞ 1 ) $ 作 $ x $ 轴的平行线分别交曲线 $ y = \frac { m } { x } ( x ＞ 0 ) $ 和 $ y = - \frac { m } { x } ( x ＜ 0 ) $ 于 $ M $，$ N $ 两点.
（1）求 $ m $ 的值及直线 $ l $ 的表达式.
（2）是否存在实数 $ p $，使得 $ S _ { \triangle A M N } = 4 S _ { \triangle A P M } $？若存在，请求出所有满足条件的 $ p $ 的值；若不存在，请说明理由.

答案：
(1)m=2,直线l的表达式为y=x−1.
(2)存在.p=$\frac{1+\sqrt{13}}{2}$或$\frac{1+\sqrt{5}}{2}$,理由略.