2025年对点对题高考状元训练手册高三数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年对点对题高考状元训练手册高三数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第39页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
阅读下面的材料,完成28~30小题.
某地为践行绿水青山就是金山银山的理念,大力开展植树造林.假设一片森林原来的面积为a亩,计划每年种植一些树苗,且森林面积的年增长率相同,当面积是原来的3倍时,所用时间是10年.
28.该片森林面积的年增长率是 ( )
$A.3^(1/10) B.3^(1/10) - 1 $
$C.3^(1/11) D.3^(1/11) - 1$
29.若到今年为止,森林面积为原来的$\sqrt{3}$倍,则该地已经植树造林 ( )
A.5年 B.6年
C.7年 D.8年
30.若森林面积至少达到6a亩,则至少需要植树造林多少年(精确到整数) ( )
(参考数据:lg2 = 0.3010,lg3 = 0.4771)
A.15年 B.16年
C.17年 D.18年
某地为践行绿水青山就是金山银山的理念,大力开展植树造林.假设一片森林原来的面积为a亩,计划每年种植一些树苗,且森林面积的年增长率相同,当面积是原来的3倍时,所用时间是10年.
28.该片森林面积的年增长率是 ( )
$A.3^(1/10) B.3^(1/10) - 1 $
$C.3^(1/11) D.3^(1/11) - 1$
29.若到今年为止,森林面积为原来的$\sqrt{3}$倍,则该地已经植树造林 ( )
A.5年 B.6年
C.7年 D.8年
30.若森林面积至少达到6a亩,则至少需要植树造林多少年(精确到整数) ( )
(参考数据:lg2 = 0.3010,lg3 = 0.4771)
A.15年 B.16年
C.17年 D.18年
答案:
28.B 设森林面积的年增长率为x,则$a(1 + x)^10 = 3a,$解得$x = 3^(1/10) - 1,$故选B.
@@29.A 设该地已经植树造林n年,则a(1 + x)^n = $\sqrt{3}a$,即3^(n/10) = $\sqrt{3}$,解得n = 5,所以该地已经植树造林5年,故选A.
@@30.C 设为使森林面积至少达到6a亩,至少需要植树造林m年,则a(1 + x)^m≥6a,
∴3^(m/10)≥6,
∴$\frac{m}{10}$≥log₃6 = log₃2 + log₃3 = 1+$\frac{lg 2}{lg 3}$≈1+$\frac{0.3010}{0.4771}$≈1.63,
∴m≥16.3,即m取17,故选C.
@@29.A 设该地已经植树造林n年,则a(1 + x)^n = $\sqrt{3}a$,即3^(n/10) = $\sqrt{3}$,解得n = 5,所以该地已经植树造林5年,故选A.
@@30.C 设为使森林面积至少达到6a亩,至少需要植树造林m年,则a(1 + x)^m≥6a,
∴3^(m/10)≥6,
∴$\frac{m}{10}$≥log₃6 = log₃2 + log₃3 = 1+$\frac{lg 2}{lg 3}$≈1+$\frac{0.3010}{0.4771}$≈1.63,
∴m≥16.3,即m取17,故选C.
根据下面的题设,完成31~33小题.
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E,F,G分别是AB,PC,CD的中点,PA = AB = AD = 1.
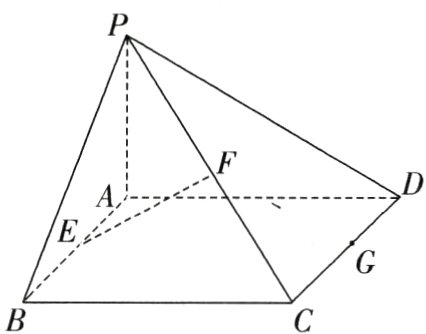
31.下列结论不正确的是 ( )
A.EF//平面PAD B.EF⊥CD
C.EF⊥PD D.EF = PD
32.直线AP与平面PCD所成的角是 ( )
A.30° B.45°
C.60° D.90°
33.直线PD与AC成的角是 ( )
A.30° B.45°
C.60° D.90°
如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,E,F,G分别是AB,PC,CD的中点,PA = AB = AD = 1.

31.下列结论不正确的是 ( )
A.EF//平面PAD B.EF⊥CD
C.EF⊥PD D.EF = PD
32.直线AP与平面PCD所成的角是 ( )
A.30° B.45°
C.60° D.90°
33.直线PD与AC成的角是 ( )
A.30° B.45°
C.60° D.90°
答案:
31.D 取PD中点H,连FH,AH,则FH//CD且FH = $\frac{1}{2}$CD.又
∵矩形ABCD,E为AB中点,
∴AE//CD且AE = $\frac{1}{2}$CD,
∴FH//AE且FH = AE,
∴AEFH为平行四边形,
∴EF//AH.又
∵EF⊄平面PAD,AH⊂平面PAD,
∴EF//平面PAD,选项A正确;
∵CD⊥AD,CD⊥PA,PA∩AD = A,PA⊂平面PAD,AD⊂平面PAD
∴CD⊥平面PAD.又
∵AH⊂平面PAD,
∴CD⊥AH.
∵EF//AH,
∴CD⊥EF.
∵PA = AB = AD = 1,H是中点,
∴AH⊥PD,且AH = $\frac{1}{2}$PD.
∵EF//AH且EF = AH,
∴EF⊥PD,且EF = $\frac{1}{2}$PD,
∴选项B,C正确,D错误,故选D.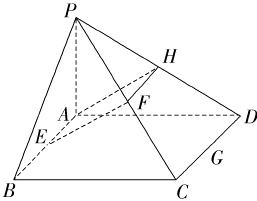
@@32.B 易知AH⊥CD,AH⊥PD,CD∩PD = D,CD、PD⊂平面PCD,则AH⊥平面PCD,所以PH是PA在平面PCD上的射影,则∠APH为直线AP与平面PCD所成的角,
∵PA = AD,
∴∠APH = 45°,即直线AP与平面PCD所成的角为45°,故选B.
@@33.C 设AC、BD交于点O,取PB的中点M,连接AM,OM,则OM//PD,OM = $\frac{1}{2}$PD = $\frac{\sqrt{2}}{2}$,则OM与AC所成的角就是PD与AC所成的角.又
∵PB = $\sqrt{2}$,AM = $\frac{1}{2}$PB = $\frac{\sqrt{2}}{2}$,OA = $\frac{1}{2}$AC = $\frac{\sqrt{2}}{2}$,则OA = AM = OM,则△OAM为正三角形,则∠AOM = 60°,即直线PD与AC所成的角为60°,故选C.
31.D 取PD中点H,连FH,AH,则FH//CD且FH = $\frac{1}{2}$CD.又
∵矩形ABCD,E为AB中点,
∴AE//CD且AE = $\frac{1}{2}$CD,
∴FH//AE且FH = AE,
∴AEFH为平行四边形,
∴EF//AH.又
∵EF⊄平面PAD,AH⊂平面PAD,
∴EF//平面PAD,选项A正确;
∵CD⊥AD,CD⊥PA,PA∩AD = A,PA⊂平面PAD,AD⊂平面PAD
∴CD⊥平面PAD.又
∵AH⊂平面PAD,
∴CD⊥AH.
∵EF//AH,
∴CD⊥EF.
∵PA = AB = AD = 1,H是中点,
∴AH⊥PD,且AH = $\frac{1}{2}$PD.
∵EF//AH且EF = AH,
∴EF⊥PD,且EF = $\frac{1}{2}$PD,
∴选项B,C正确,D错误,故选D.

@@32.B 易知AH⊥CD,AH⊥PD,CD∩PD = D,CD、PD⊂平面PCD,则AH⊥平面PCD,所以PH是PA在平面PCD上的射影,则∠APH为直线AP与平面PCD所成的角,
∵PA = AD,
∴∠APH = 45°,即直线AP与平面PCD所成的角为45°,故选B.
@@33.C 设AC、BD交于点O,取PB的中点M,连接AM,OM,则OM//PD,OM = $\frac{1}{2}$PD = $\frac{\sqrt{2}}{2}$,则OM与AC所成的角就是PD与AC所成的角.又
∵PB = $\sqrt{2}$,AM = $\frac{1}{2}$PB = $\frac{\sqrt{2}}{2}$,OA = $\frac{1}{2}$AC = $\frac{\sqrt{2}}{2}$,则OA = AM = OM,则△OAM为正三角形,则∠AOM = 60°,即直线PD与AC所成的角为60°,故选C.

查看更多完整答案,请扫码查看


