2025年对点对题高考状元训练手册高三数学人教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年对点对题高考状元训练手册高三数学人教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
25.已知△ABC中,角A,B,C所对的边分别为a,b,c,若csin A=$\sqrt{3}$acos C,c=3$\sqrt{3}$,ab=18,则a + b的值是 ( )
A.6$\sqrt{2}$
B.6$\sqrt{3}$
C.9
D.11
A.6$\sqrt{2}$
B.6$\sqrt{3}$
C.9
D.11
答案:
C
∵c sin A = $\sqrt{3}$a cos C,
∴sin C sin A = $\sqrt{3}$sin A cos C,
∵sin A≠0,
∴tan C = $\sqrt{3}$.
∴0 < C < π,
∴C = $\frac{\pi}{3}$,根据余弦定理可得c$^{2}$ = a$^{2}$ + b$^{2}$ - 2ab cos C = (a + b)$^{2}$ - 3ab,
∴(3$\sqrt{3}$)$^{2}$ = (a + b)$^{2}$ - 3×18,
∴a + b = 9. 故选C.
∵c sin A = $\sqrt{3}$a cos C,
∴sin C sin A = $\sqrt{3}$sin A cos C,
∵sin A≠0,
∴tan C = $\sqrt{3}$.
∴0 < C < π,
∴C = $\frac{\pi}{3}$,根据余弦定理可得c$^{2}$ = a$^{2}$ + b$^{2}$ - 2ab cos C = (a + b)$^{2}$ - 3ab,
∴(3$\sqrt{3}$)$^{2}$ = (a + b)$^{2}$ - 3×18,
∴a + b = 9. 故选C.
26.已知函数y=sin(ωx + φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则 ( )

A.ω=1,φ=$\frac{π}{6}$
B.ω=1,φ=-$\frac{π}{6}$
C.ω=2,φ=$\frac{π}{6}$
D.ω=2,φ=-$\frac{π}{6}$

A.ω=1,φ=$\frac{π}{6}$
B.ω=1,φ=-$\frac{π}{6}$
C.ω=2,φ=$\frac{π}{6}$
D.ω=2,φ=-$\frac{π}{6}$
答案:
D 依题意得T = $\frac{2\pi}{\omega}$ = 4×($\frac{7\pi}{12}$ - $\frac{\pi}{3}$) = π,所以ω = 2. 又sin(2×$\frac{\pi}{3}$ + φ) = sin($\frac{2\pi}{3}$ + φ) = 1,所以$\frac{2\pi}{3}$ + φ = $\frac{\pi}{2}$ + 2kπ,k∈Z. 所以φ = - $\frac{\pi}{6}$ + 2kπ,k∈Z,由|φ| < $\frac{\pi}{2}$,得φ = - $\frac{\pi}{6}$. 故选D.
27.如图所示,在正三棱柱ABC - A1B1C1中,若AB=$\sqrt{2}$BB1,则异面直线AB1与BC1所成的角的大小是 ( )

A.60°
B.75°
C.90°
D.105°

A.60°
B.75°
C.90°
D.105°
答案:
C 设BB$_{1}$ = 1,如图,延长CC$_{1}$至点C$_{2}$,使C$_{1}$C$_{2}$ = CC$_{1}$ = 1,连接B$_{1}$C$_{2}$,则B$_{1}$C$_{2}$//BC$_{1}$,所以∠AB$_{1}$C$_{2}$(或其补角)为异面直线AB$_{1}$与BC$_{1}$所成的角. 连接AC$_{2}$,易知AB$_{1}$ = $\sqrt{3}$,B$_{1}$C$_{2}$ = $\sqrt{3}$,AC$_{2}$ = $\sqrt{6}$,所以AC$_{2}^{2}$ = AB$_{1}^{2}$ + B$_{1}$C$_{2}^{2}$,则∠AB$_{1}$C$_{2}$ = 90°,即异面直线AB$_{1}$与BC$_{1}$所成的角的大小为90°.

C 设BB$_{1}$ = 1,如图,延长CC$_{1}$至点C$_{2}$,使C$_{1}$C$_{2}$ = CC$_{1}$ = 1,连接B$_{1}$C$_{2}$,则B$_{1}$C$_{2}$//BC$_{1}$,所以∠AB$_{1}$C$_{2}$(或其补角)为异面直线AB$_{1}$与BC$_{1}$所成的角. 连接AC$_{2}$,易知AB$_{1}$ = $\sqrt{3}$,B$_{1}$C$_{2}$ = $\sqrt{3}$,AC$_{2}$ = $\sqrt{6}$,所以AC$_{2}^{2}$ = AB$_{1}^{2}$ + B$_{1}$C$_{2}^{2}$,则∠AB$_{1}$C$_{2}$ = 90°,即异面直线AB$_{1}$与BC$_{1}$所成的角的大小为90°.

阅读下面的材料完成28~30小题.
将高三某班60名学生参加某次数学模拟考试所得的成绩(成绩均为整数)整理后画出频率分布直方图如图.
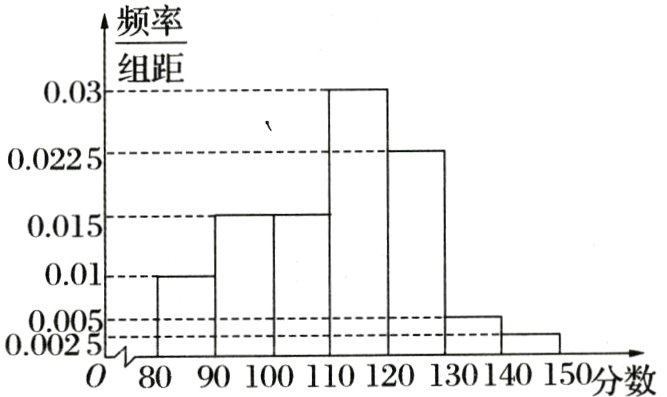
28.该班模拟考试中,成绩在[100,120)的人数为 ( )
A.9
B.18
C.27
D.30
29.该班模拟考试中及格率(90及以上为及格)估计值为 ( )
A.90%
B.65%
C.75%
D.80%
30.该班模拟考试中,80%分位数为 ( )
A.123.44
B.124.44
C.125
D.126.44
将高三某班60名学生参加某次数学模拟考试所得的成绩(成绩均为整数)整理后画出频率分布直方图如图.

28.该班模拟考试中,成绩在[100,120)的人数为 ( )
A.9
B.18
C.27
D.30
29.该班模拟考试中及格率(90及以上为及格)估计值为 ( )
A.90%
B.65%
C.75%
D.80%
30.该班模拟考试中,80%分位数为 ( )
A.123.44
B.124.44
C.125
D.126.44
答案:
C 成绩在[100,110)的人数为60×0.015×10 = 9(人).成绩在[110,120)的人数为60×0.03×10 = 18(人).所以,成绩在[100,120)的人数为9 + 18 = 27(人).
@@A 成绩在[80,90)的频率为0.01×10 = 0.1.所以估计及格率为1 - 0.1 = 0.9 = 90%.
@@B 由频率分布直方图可知,分数在120分以下的学生所占的比例为(0.01 + 0.015 + 0.015 + 0.03)×10×100% = 70%,分数在130分以下的学生所占的比例为(0.01 + 0.015 + 0.015 + 0.03 + 0.022 5)×10×100% = 92.5%,因此80%分位数一定位于[120,130)内. 因为120 + $\frac{0.80 - 0.70}{0.925 - 0.70}$×10≈124.44,所以此班的模拟考试成绩的80%分位数约为124.44.
@@A 成绩在[80,90)的频率为0.01×10 = 0.1.所以估计及格率为1 - 0.1 = 0.9 = 90%.
@@B 由频率分布直方图可知,分数在120分以下的学生所占的比例为(0.01 + 0.015 + 0.015 + 0.03)×10×100% = 70%,分数在130分以下的学生所占的比例为(0.01 + 0.015 + 0.015 + 0.03 + 0.022 5)×10×100% = 92.5%,因此80%分位数一定位于[120,130)内. 因为120 + $\frac{0.80 - 0.70}{0.925 - 0.70}$×10≈124.44,所以此班的模拟考试成绩的80%分位数约为124.44.
根据下面的题设,完成31~33小题.
《九章算术·商功》记载了一个古代数学名词“堑堵”.即两底面为直角三角形的直棱柱,即长方体的斜截平分体.如图所示,堑堵(即直三棱柱)ABC - DEF中,AB⊥AC,AB = AC = 2,AD = 4,G是FC的中点.
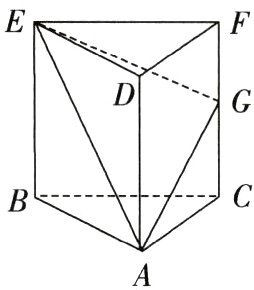
31.直线BE与AG的夹角为 ( )
A.$\frac{π}{6}$
B.$\frac{π}{3}$
C.$\frac{π}{4}$
D.$\frac{π}{2}$
32.△AGE的形状为 ( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
33.点D到平面AGE的距离为 ( )
A.$\frac{\sqrt{6}}{3}$
B.$\frac{\sqrt{6}}{2}$
C.$\frac{\sqrt{5}}{4}$
D.$\frac{2\sqrt{6}}{3}$
《九章算术·商功》记载了一个古代数学名词“堑堵”.即两底面为直角三角形的直棱柱,即长方体的斜截平分体.如图所示,堑堵(即直三棱柱)ABC - DEF中,AB⊥AC,AB = AC = 2,AD = 4,G是FC的中点.

31.直线BE与AG的夹角为 ( )
A.$\frac{π}{6}$
B.$\frac{π}{3}$
C.$\frac{π}{4}$
D.$\frac{π}{2}$
32.△AGE的形状为 ( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
33.点D到平面AGE的距离为 ( )
A.$\frac{\sqrt{6}}{3}$
B.$\frac{\sqrt{6}}{2}$
C.$\frac{\sqrt{5}}{4}$
D.$\frac{2\sqrt{6}}{3}$
答案:
C
∵BE//CG,
∴∠AGC即为BE与AG所成的角(或其补角),
∵G为CF的中点,CF = AD = 4,AC = 2,
∴AC = CG,又CF⊥平面ABC,
∴∠AGC = $\frac{\pi}{4}$.
@@B 依题意可知,AG = 2$\sqrt{2}$,EG = 2$\sqrt{3}$,EA = 2$\sqrt{5}$,
∴AG$^{2}$ + EG$^{2}$ = EA$^{2}$,
∴AG⊥GE,
∴△AGE为直角三角形.
@@D 设点D到平面AGE的距离为h,则由V$_{D - AGE}$ = V$_{E - ADG}$可知$\frac{1}{3}$h×$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{3}$ = $\frac{1}{3}$×2×$\frac{1}{2}$×2×4,则h = $\frac{2\sqrt{6}}{3}$.
∵BE//CG,
∴∠AGC即为BE与AG所成的角(或其补角),
∵G为CF的中点,CF = AD = 4,AC = 2,
∴AC = CG,又CF⊥平面ABC,
∴∠AGC = $\frac{\pi}{4}$.
@@B 依题意可知,AG = 2$\sqrt{2}$,EG = 2$\sqrt{3}$,EA = 2$\sqrt{5}$,
∴AG$^{2}$ + EG$^{2}$ = EA$^{2}$,
∴AG⊥GE,
∴△AGE为直角三角形.
@@D 设点D到平面AGE的距离为h,则由V$_{D - AGE}$ = V$_{E - ADG}$可知$\frac{1}{3}$h×$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{3}$ = $\frac{1}{3}$×2×$\frac{1}{2}$×2×4,则h = $\frac{2\sqrt{6}}{3}$.
查看更多完整答案,请扫码查看


