第71页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
10. 如图,四边形 ABCD 是正方形,以 CD 为边向正方形外作等边△CDE,AC 与 BE 相交于点 F,则∠AFD 的度数为 ( )
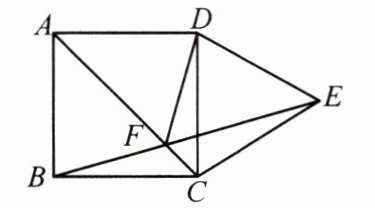
A. 65° B. 60° C. 50° D. 45°

A. 65° B. 60° C. 50° D. 45°
答案:
B
11. (兴安盟中考)如图,AD 是△ABC 的角平分线,DE⊥AB,DF⊥AC,垂足分别是 E、F,连结 EF,EF 与 AD 相交于点 H。
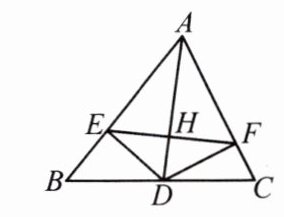
(1) 求证:AD⊥EF。
(2) △ABC 满足什么条件时,四边形 AEDF 是正方形?说明理由。

(1) 求证:AD⊥EF。
(2) △ABC 满足什么条件时,四边形 AEDF 是正方形?说明理由。
答案:
(1)证明:
∵AD是△ABC的角平分线,
∴∠EAD = ∠FAD.
∵DE⊥AB,DF⊥AC,
∴∠AED = ∠AFD = 90°.
在△AED与△AFD中,
$\begin{cases}∠EAD = ∠FAD\\∠AED = ∠AFD\\AD = AD\end{cases}$
∴△AED ≌ △AFD(A.A.S.),
∴AE = AF,
∴AD⊥EF.
(2)解:△ABC满足∠BAC = 90°时,四边形AEDF是正方形.
理由:
∵∠AED = ∠AFD = ∠BAC = 90°,
∴四边形AEDF是矩形.
∵EF⊥AD,
∴矩形AEDF是正方形.
(1)证明:
∵AD是△ABC的角平分线,
∴∠EAD = ∠FAD.
∵DE⊥AB,DF⊥AC,
∴∠AED = ∠AFD = 90°.
在△AED与△AFD中,
$\begin{cases}∠EAD = ∠FAD\\∠AED = ∠AFD\\AD = AD\end{cases}$
∴△AED ≌ △AFD(A.A.S.),
∴AE = AF,
∴AD⊥EF.
(2)解:△ABC满足∠BAC = 90°时,四边形AEDF是正方形.
理由:
∵∠AED = ∠AFD = ∠BAC = 90°,
∴四边形AEDF是矩形.
∵EF⊥AD,
∴矩形AEDF是正方形.
12. (荆门中考)如图,点 E 是正方形 ABCD 的边 BC 上的动点,∠AEF = 90°,且 EF = AE,FH⊥BH。
(1) 求证:BE = CH。
(2) 连结 DF,若 AB = 3,BE = x,用含 x 的代数式表示 DF 的长。
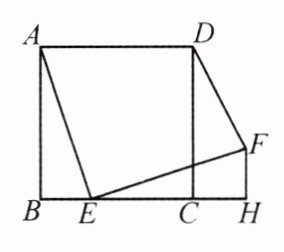
(1) 求证:BE = CH。
(2) 连结 DF,若 AB = 3,BE = x,用含 x 的代数式表示 DF 的长。

答案:
(1)证明:在正方形ABCD中,
∠B = 90°,AB = BC,
∵FH⊥BH,
∴∠H = 90° = ∠B,∠EFH = 90° - ∠FEH.
∵∠AEF = 90°,
∴∠AEB = 90° - ∠FEH.
∴∠AEB = ∠EFH.
在△ABE和△EHF中,
$\begin{cases}∠B = ∠H\\∠AEB = ∠EFH\\AE = EF\end{cases}$
∴△ABE ≌ △EHF(A.A.S.).
∴EH = AB = BC,BE = FH.
∴EH - EC = BC - EC,即CH = BE.
(2)解:过点F作FP⊥CD于点P,如图,
∵∠H = ∠DCH = ∠FPC = 90°,
∴四边形PCHF是矩形.
 由
由
(1)知,BE = FH = CH,
∴四边形PCHF是正方形.
∴PF = CP = CH = BE = x.
∵DC = AB = 3,
∴DP = DC - CP = 3 - x.
在Rt△DPF中,DF = $\sqrt{DP^{2}+PF^{2}}$
∴DF = $\sqrt{(3 - x)^{2}+x^{2}}$ = $\sqrt{2x^{2}-6x + 9}$
(1)证明:在正方形ABCD中,
∠B = 90°,AB = BC,
∵FH⊥BH,
∴∠H = 90° = ∠B,∠EFH = 90° - ∠FEH.
∵∠AEF = 90°,
∴∠AEB = 90° - ∠FEH.
∴∠AEB = ∠EFH.
在△ABE和△EHF中,
$\begin{cases}∠B = ∠H\\∠AEB = ∠EFH\\AE = EF\end{cases}$
∴△ABE ≌ △EHF(A.A.S.).
∴EH = AB = BC,BE = FH.
∴EH - EC = BC - EC,即CH = BE.
(2)解:过点F作FP⊥CD于点P,如图,
∵∠H = ∠DCH = ∠FPC = 90°,
∴四边形PCHF是矩形.
 由
由(1)知,BE = FH = CH,
∴四边形PCHF是正方形.
∴PF = CP = CH = BE = x.
∵DC = AB = 3,
∴DP = DC - CP = 3 - x.
在Rt△DPF中,DF = $\sqrt{DP^{2}+PF^{2}}$
∴DF = $\sqrt{(3 - x)^{2}+x^{2}}$ = $\sqrt{2x^{2}-6x + 9}$
13. 如图,在△ABC 中,∠BAC = 45°,AD⊥BC 于点 D,将△ACD 沿 AC 折叠为△ACF,将△ABD 沿 AB 折叠为△ABG,延长 FC 和 GB 相交于点 H。
(1) 求证:四边形 AFHG 是正方形。
(2) 若 AD = 12,CD = 4,求 BD 的长。
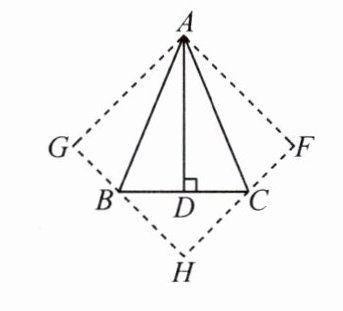
(1) 求证:四边形 AFHG 是正方形。
(2) 若 AD = 12,CD = 4,求 BD 的长。

答案:
(1)证明:
∵AD⊥BC,
∴∠ADB = ∠ADC = 90°.由折叠的性质可知AG = AD = AF,∠G = ∠ADB = ∠ADC = ∠F = 90°,∠BAG = ∠BAD,∠CAF = ∠CAD.
∴∠BAG + ∠CAF = ∠BAD + ∠CAD = ∠BAC = 45°.
∴∠GAF = ∠BAG + ∠CAF + ∠BAC = 90°.
∴∠G = ∠F = ∠GAF = 90°.
∴四边形AFHG是矩形.
又
∵AG = AF,
∴四边形AFHG是正方形.
(2)解:
∵四边形AFHG是正方形,
∴∠BHC = 90°,GH = HF = AF = AD = 12.由折叠的性质可知GB = BD,CF = CD = 4,则CH = HF - CF = 8.设BD的长为x,则BH = GH - GB = 12 - x,BC = BD + CD = x + 4.
在Rt△BCH中,BH² + CH² = BC²,即(12 - x)² + 8² = (x + 4)²,解得x = 6.故BD的长为6.
(1)证明:
∵AD⊥BC,
∴∠ADB = ∠ADC = 90°.由折叠的性质可知AG = AD = AF,∠G = ∠ADB = ∠ADC = ∠F = 90°,∠BAG = ∠BAD,∠CAF = ∠CAD.
∴∠BAG + ∠CAF = ∠BAD + ∠CAD = ∠BAC = 45°.
∴∠GAF = ∠BAG + ∠CAF + ∠BAC = 90°.
∴∠G = ∠F = ∠GAF = 90°.
∴四边形AFHG是矩形.
又
∵AG = AF,
∴四边形AFHG是正方形.
(2)解:
∵四边形AFHG是正方形,
∴∠BHC = 90°,GH = HF = AF = AD = 12.由折叠的性质可知GB = BD,CF = CD = 4,则CH = HF - CF = 8.设BD的长为x,则BH = GH - GB = 12 - x,BC = BD + CD = x + 4.
在Rt△BCH中,BH² + CH² = BC²,即(12 - x)² + 8² = (x + 4)²,解得x = 6.故BD的长为6.
查看更多完整答案,请扫码查看


