《2025年一线调研学业测评八年级数学下册华师大版》

12. （宁夏中考）已知点 A(x₁, y₁)、B(x₂, y₂)在直线 y = kx + b(k≠0)上，当 x₁＜x₂ 时，y₂＞y₁，且 kb＞0，则在平面直角坐标系内，它的图象大致是（ ）

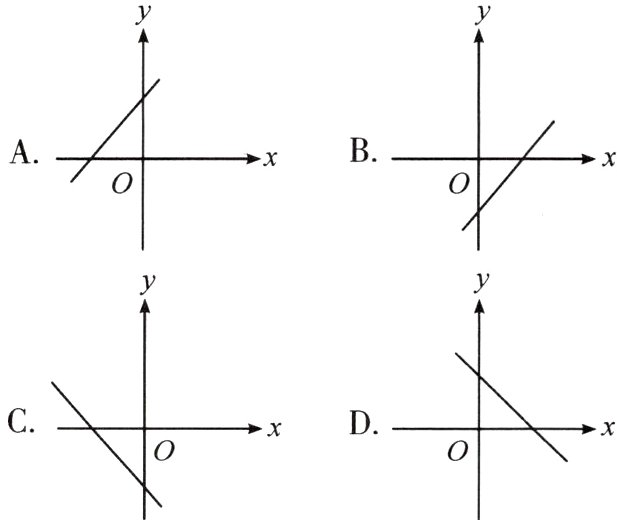
答案： A

13. 若点 A(x₁, −1)、B(x₂, −3)、C(x₃, 4)在一次函数 y = −2x + m(m 是常数)的图象上，则 x₁、x₂、x₃ 的大小关系是（ ）
A. x₁＞x₂＞x₃　　　
　B. x₂＞x₁＞x₃
C. x₁＞x₃＞x₂　　　
　D. x₃＞x₂＞x₁

答案： B

14. 一次函数 y = mx + |m − 1| 的图象过点(0, 2)，且 y 随 x 的增大而增大，则 m =（ ）
A. −1　
　B. 3　
　C. 1　
　D. −1 或 3

答案： B

15. 已知关于 x 的一次函数 y = (3a − 7)x + a − 2 的图象与 y 轴的交点在 x 轴的上方，且 y 随 x 的增大而减小，则 a 的取值范围是________.

答案： 2 ＜ a ＜ $\frac{7}{3}$

16. 已知一次函数 y = ax − a + 1(a 为常数，且 a≠0).
(1) 若点(−$\frac{1}{2}$, 3)在一次函数 y = ax − a + 1 的图象上，求 a 的值.
(2) 当−1≤x≤2 时，函数有最大值 2，请求出 a 的值.

答案： 解:
(1)把(-$\frac{1}{2}$,3)代入y = ax - a + 1，得-$\frac{1}{2}$a - a + 1 = 3，解得a = -$\frac{4}{3}$.　
(2)①当a ＞ 0时，y随x的增大而增大.
　
∵ -1 ≤ x ≤ 2，
　
∴当x = 2时，y有最大值2.把x = 2、y = 2代入函数关系式，得2a - a + 1 = 2，解得a = 1.　②当a ＜ 0时，y随x的增大而减小.
∵ -1 ≤ x ≤ 2，
∴当x = -1时，y有最大值2.把x = -1、y = 2代入函数关系式，得 - a - a + 1 = 2，解得a = -$\frac{1}{2}$.　综上所述，a的值为1或 -$\frac{1}{2}$.

17. 问题：探究函数 y = |x − 1| + 1 的图象与性质.
小东根据学习一次函数的经验，对函数 y = |x − 1| + 1 的图象与性质进行了探究：
(1) 在函数 y = |x − 1| + 1 中，自变量 x 可以是任意实数，下表是 y 与 x 的几组对应值：

①表格中 m 的值为______；
②在平面直角坐标系中画出该函数的图象.
(2) 结合函数图象，写出该函数的两条性质.

答案：
解:
(1)①4　②函数图象如图所示.
(2)①函数图象关于直线x = 1对称；②函数当x = 1时有最小值1.(答案不唯一)