《2025年一线调研学业测评八年级数学下册华师大版》

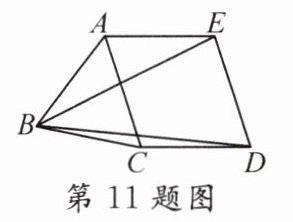
11. 如图，已知凸五边形ABCDE的边长均相等，且∠DBE = ∠ABE + ∠CBD，AC = 1，则BD必定满足　　　　　　　　　(　　　)


A. BD＜2　　　　
　B. BD = 2
C. BD＞2　　　　
　D. 以上情况均有可能

答案： A　[解析]根据∠DBE = ∠ABE + ∠CBD,AB = AE = BC = CD,且△BED的内角和为180°,得出∠AED + ∠CDE = 180°.故AE//CD.又由AE = CD,推出四边形AEDC为平行四边形，进而推出DE = AC = 1,则BC = CD = DE = 1,推出BD＜BC + CD = 2.

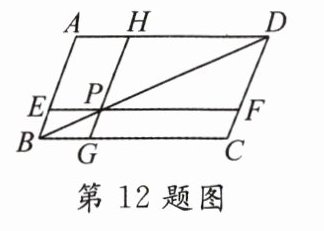
12. 如图，在▱ABCD中，过对角线BD上一点P作EF//BC，GH//AB，且CG = 2BG，S△BPG = 1，则S▱AEPH = ______.

答案： 4

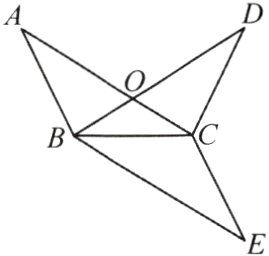
13. 如图，已知∠A = ∠D，AB = DC，AC、BD相交于点O.
(1) 求证:△AOB≌△DOC.
(2) 若AB = BC，∠A = 32°，则∠AOB = ____.
(3) 作△BDC关于直线BC的对称图形△BEC，求证:四边形ABEC是平行四边形.

答案：
(1)证明:
∵∠A = ∠D,AB = DC,∠AOB = ∠DOC,
∴△AOB≌△DOC.
(2)64°
(3)证明:由
(1)知,△AOB≌△DOC,
∴OB = OC.
∴∠OCB = ∠OBC.又
∵∠A = ∠D,AB = DC,
∴△ABC≌△DCB.
∴AC = DB.
∵△BDC和△BEC关于直线BC对称，
∴DC = EC,DB = EB.
∴AB = EC,AC = EB.
∴四边形ABEC是平行四边形.

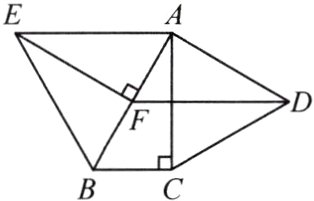
14. 如图，分别以Rt△ABC的直角边AC及斜边AB为一边向外作等边三角形ACD及等边三角形ABE，已知∠BAC = 30°，EF⊥AB，垂足为F，连结DF. 求证:
(1) AC = EF.
(2) 四边形ADFE是平行四边形.

答案： 证明:
(1)
∵在Rt△ABC中,∠BAC = 30°,
∴AB = 2BC.
又
∵△ABE是等边三角形，EF⊥AB，
∴AE = AB = 2AF.
∴AF = BC.
在Rt△AFE和Rt△BCA中,
{AF = BC,
AE = BA,
∴Rt△AFE≌Rt△BCA(H.L.).
∴EF = AC.
(2)
∵△ACD是等边三角形，
∴∠DAC = 60°,AC = AD.
∴∠DAB = ∠DAC + ∠BAC = 90° = ∠AFE.
∴EF//AD.
又
∵AC = EF,
∴EF = AD.
∴四边形ADFE是平行四边形.

15. 如图是某城市部分街道示意图，其中CE垂直平分AF，AB//CD，BC//DF. 从B站乘车到E站只有两条路线有直接到达的公交车，路线①是B→D→A→E，路线②是B→C→F→E，请比较两条路线路程的长短，并给出理由.

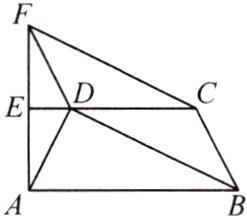
答案：
解:这两条路线的路程相等.理由如下:
如图，延长FD交AB于点G.
∵BC//DF,AB//DC,
∴四边形BCDG是平行四边形.
∴DG = BC.
∵CE垂直平分AF,
∴DF = DA,FE = AE,∠DEF = 90°.又
∵AB//CD,
∴∠GAF = ∠DEF = 90°.
∴∠DAE + ∠DAG = 90°,∠AFG + ∠AGF = 90°.
∵DF = DA,
∴∠AFG = ∠DAE.
∴∠DAG = ∠AGF.
∴AD = DG = DF.
∴AD = BC,DF = BC.
∴四边形BCFD是平行四边形.
∴CF = BD.
∴路线①的路程BD + DA + AE = 路线②的路程BC + CF + FE.