《2025年一线调研学业测评八年级数学下册华师大版》

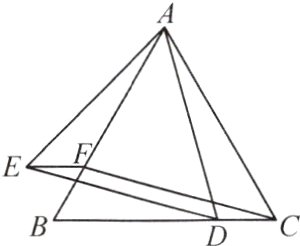
10. 如图,△ABC为等边三角形,D、F分别为BC、AB上的点,且CD = BF.
(1)求证:△ACD≌△CBF.
(2)以AD为边作等边三角形ADE,求证:四边形CDEF是平行四边形.

答案： 证明:
(1)
∵△ABC为等边三角形，
∴∠ACD = ∠B = 60°，
AC = CB.又
∵CD = BF，
∴△ACD ≌ △CBF.
(2)
∵△ACD ≌ △CBF，
∴∠CAD = ∠BCF，AD = CF.
∵△ADE为等边三角形，
∴AD = DE，∠ADE = 60°.
∴DE = CF.
∵∠ACD = ∠ADE = 60°，∠ADB = ∠ADE + ∠BDE = ∠ACD + ∠CAD，
∴∠CAD = ∠BDE.
又
∵∠CAD = ∠BCF，
∴∠BDE = ∠BCF.
∴DE//CF.
又
∵DE = CF，
∴四边形CDEF是平行四边形.

11. 如图,在Rt△ABC中,∠ACB = 90°.
(1)尺规作图:作∠BAC的平分线AM交BC于点D.(只保留作图痕迹,不写作法)
(2)在(1)所作的图形中,将Rt△ABC沿某条直线折叠，使点A与点D重合，折痕EF交AC于点E,交AD于点O,交AB于点F,连结DE、DF,再展回到原图形，得到四边形AEDF.
①试说明四边形AEDF为平行四边形;②若AB = 10,BC = 8,在折痕EF上有一动点P,则PC十PD的最小值为______.

答案： 解:
(1)如图所示.
(2)①由折叠可知，EF垂直平分AD，
∴AO = OD，∠AOE = ∠AOF.又
∵AD平分∠BAC，
∴∠EAO = ∠FAO.
∵AO = AO，
∴△AEO ≌ △AFO.
∴OE = OF.
∴四边形AEDF为平行四边形.
②6

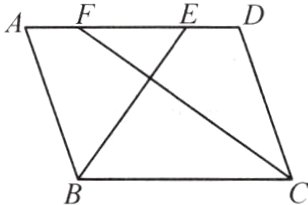
12. 如图,在▱ABCD中，AB = 5,BC = 8,∠ABC和∠BCD的平分线分别交AD于点E、F,若BE = 6,则CF = ______.

答案： 8

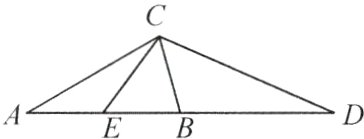
13. 如图，已知AB = AC,B是AD的中点,E是AB的中点.求证:CD = 2CE.

答案： 证明:如图，延长CE至点F，使EF = CE，连结AF、BF，
则CF = 2CE；
∵E是AB的中点，
∴AE = BE.
∴四边形AFBC是平行四边形.
∴AC//BF，AC = BF.
∴∠CAB = ∠FBA.又
∵AB = AC，B是AD的中点，
∴∠BCA = ∠ABC，AC = BD.
∴BD = BF.
∵∠DBC = ∠BCA + ∠CAB，∠FBC = ∠FBA + ∠ABC，
∴∠DBC = ∠FBC.
又
∵BC = BC，
∴△DBC ≌ △FBC.
∴CD = CF.
∴CD = 2CE.

14. 方程思想如图,已知BD垂直平分AC,∠BCD = ∠ADF,AF⊥AC.
(1)求证:四边形ABDF是平行四边形.
(2)若AF = DF = 5,AD = 6,求AC的长.

答案：
(1)证明:
∵BD垂直平分AC，
∴AB = CB，AD = CD.又
∵DB = DB，
∴△ADB ≌ △CDB.
∴∠BAD = ∠BCD.又
∵∠BCD = ∠ADF，
∴∠BAD = ∠ADF.
∴AB//FD.
∵BD⊥AC，AF⊥AC，
∴AF//BD.
∴四边形ABDF是平行四边形.
(2)解:
∵四边形ABDF是平行四边形，AF = DF = 5，
∴AB = BD = 5.设BE = x，则DE = 5 - x.
∵BD⊥AE，
∴AB² - BE² = AD² - DE²，即5² - x² = 6² - (5 - x)².解得x = $\frac{7}{5}$.
∴AE = $\sqrt{AB² - BE²}$ = $\frac{24}{5}$.
∴AC = 2AE = $\frac{48}{5}$.