《2025年一线调研学业测评八年级数学下册华师大版》

8. 函数y = - $\frac{1}{|x|}$的大致图象是(　　)

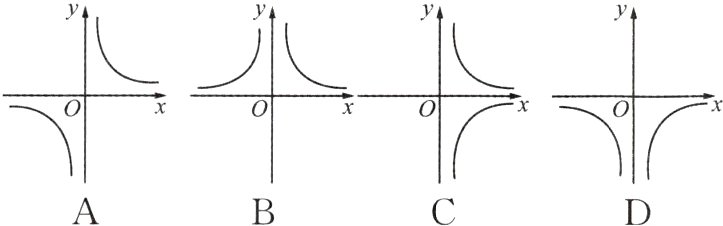
答案： D

9. 在温度不变的条件下，通过一次又一次地对汽缸顶部的活塞加压，测出每一次加压后缸内气体的体积和气体对汽缸壁所产生的压强如下表。

则可以反映y与x之间关系的式子是(　　)
A. y = 3000x　　　　　
　B. y = 6000x
C. y = $\frac{3000}{x}$　　　　　　
　D. y = $\frac{6000}{x}$

答案： D

10. 如图，A为反比例函数y = $\frac{k}{x}$(其中x＞0)图象上的一点，在x轴正半轴上有一点B，OB = 6。连结OA、AB，且OA = AB。过点B作BC⊥OB，交反比例函数y = $\frac{k}{x}$(其中x＞0)的图象于点C，连结OC交AB于点D，若S△OBC = 6，则AB的长度为(　　)

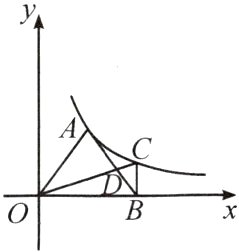
A. 4　　
　B. $\sqrt{50}$　　
　C. 5　　
　D. $\sqrt{75}$

答案： C

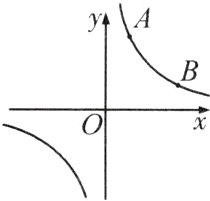
11. 反比例函数y = $\frac{k}{x}$(k为常数，且k≠0)的图象经过点A(1, 3)、B(3, m)。
(1)求反比例函数的表达式及点B的坐标。
(2)在x轴上找一点P，使PA + PB的值最小，满足条件的点P的坐标为________。

答案： 解:
(1)把A(1,3)代入y = $\frac{k}{x}$，得k = 1×3 = 3.
∴反比例函数的表达式为y = $\frac{3}{x}$.
把B(3,m)代入y = $\frac{3}{x}$，得3m = 3.解得m = 1.
∴B(3,1).
(2)($\frac{5}{2}$,0)

12. 规定:在平面直角坐标系内，某直线l1绕原点O顺时针旋转90°，得到的直线l2称为l1的“旋转垂线”。
(1)求出直线y = - x + 2的“旋转垂线”的表达式。
(2)若直线y = k1x + 1(k1≠0)的“旋转垂线”为直线y = k2x + b，求证: k1·k2 = - 1。

答案：
(1)解:直线y = -x + 2经过点(2,0)和(0,2)，则这两点绕原点O顺时针旋转90°，得到的对应点为(0,-2)和(2,0).
设直线y = -x + 2的“旋转垂线”的表达式为y = kx + m.
把(0,-2)和(2,0)代入y = kx + m，可得$\begin{cases}m = -2 \\ 2k + m = 0 \end{cases}$，
解得$\begin{cases}k = 1 \\ m = -2 \end{cases}$，
∴直线y = -x + 2的“旋转垂线”的表达式为y = x - 2.
(2)证明:直线y = k1x + 1(k1≠0)经过点(-$\frac{1}{k_1}$,0)和(0,1)，则这两点绕原点O顺时针旋转90°，得到的对应点为(0,$\frac{1}{k_1}$)和(1,0).
把(0,$\frac{1}{k_1}$)和(1,0)代入y = k2x + b，可得$\begin{cases}b = \frac{1}{k_1} \\ k2 + b = 0 \end{cases}$，
∴k2 + $\frac{1}{k_1}$ = 0.
∴k1·k2 = -1.