《2025年一线调研学业测评八年级数学下册华师大版》

1. 下列函数中，是一次函数的有　　　　(　　)
①y = −x² + 24；②y = 2x；③y = $\frac{2}{x}$；④y = −πx + π.
A. ③④　
　B. ①②　
　C. ②　
　D. ②④

答案： D

2. 等腰三角形顶角的度数y与底角的度数x之间的函数关系式及x的取值范围是　(　　)
A. y = 180 − 2x(0＜x≤180)
B. y = 180 − x(0＜x＜90)
C. y = 180 − 2x(0＜x＜90)
D. y = 180 − x(0＜x≤180)

答案： C

3. 把一个长10cm、宽5cm的长方形的长减少xcm，宽不变，得到的新长方形的面积为ycm².
(1) y与x之间的函数关系式是____________.
(2) 自变量x的取值范围是____________.

答案：
(1)y = -5x + 50
(2)0 ≤ x ＜ 10

4. 下列说法正确的是　　　　(　　)
A. 一次函数一定不是正比例函数
B. 正比例函数不一定是一次函数
C. 一次函数一定是正比例函数
D. 正比例函数一定是一次函数

答案： D

5. 已知函数y = (m − 2)x$^{m² - 3}$ + n + 2(m, n是常数)是正比例函数，则m + n的值为　　　　(　　)
A. −4或0　　　
　B. ±2
C. 0　　　　　　
　D. −4

答案： D

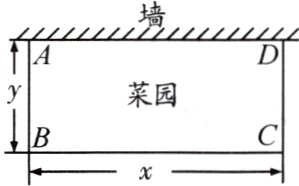
6. 李大爷要围成一个长方形菜园，菜园的一边利用足够长的墙，用篱笆围成的另外三边总长应恰好为24米，要围成的菜园是如图所示的长方形ABCD，设BC边的长为x米，AB边的长为y米，则y与x之间的函数关系式是(　　)

A. y = −2x + 24(0＜x＜12)
B. y = −$\frac{1}{2}$x + 12(0＜x＜24)
C. y = 2x − 24(0＜x＜12)
D. y = $\frac{1}{2}$x − 12(0＜x＜24)

答案： B

7. 定义{m, n}是一次函数y = mx + n的特征数. 若特征数是{4, k + 4}的一次函数又是正比例函数，则k的值是　　　　(　　)
A. −4　　
　B. 0　　　
　C. 4　　
　D. 任何数

答案： A

8. 已知函数y = (m + 1)x²−|m| + n + 4.
(1) 当m、n为何值时，此函数是一次函数？
(2) 当m、n为何值时，此函数是正比例函数？

答案： 解:
(1)根据一次函数的定义,得2 - |m| = 1.解得m = ±1.又因为m + 1 ≠ 0,即m ≠ -1,所以m = 1.所以当m = 1、n为任意实数时，此函数是一次函数.
(2)根据正比例函数的定义,得2 - |m| = 1,n + 4 = 0.解得m = ±1,n = -4.又因为m + 1 ≠ 0,即m ≠ -1,所以m = 1.所以当m = 1、n = -4时，此函数是正比例函数.

9. 某市为了鼓励居民节约用水，采用分段计费的方法按月计算每户家庭的水费. 月用水量不超过20立方米时，按2元/立方米计费；月用水量超过20立方米时，其中的20立方米仍按2元/立方米计费，超过部分按2.6元/立方米计费.
(1) 设每户家庭用水量为x立方米时，应交水费y元，分别求出当0≤x≤20和x＞20时，y与x的函数关系式.
(2) 小明家六月份缴纳水费45.2元，则该月用水量为多少立方米？

答案： 解:
(1)当0 ≤ x ≤ 20时,y = 2x;当x ＞ 20时,y = 20×2 + (x - 20)×2.6 = 2.6x - 12.
(2)因为小明家六月份缴纳水费45.2元，20×2 = 40 ＜ 45.2,所以小明家六月份用水量超过20立方米.由45.2 = 2.6x - 12,解得x = 22.故该月用水量为22立方米.