《2025年一线调研学业测评八年级数学下册华师大版》

1.下列图形能够反映四边形、平行四边形、矩形的关系的是　　　　　　　　　　　(　　　)

答案： C

2.矩形具有而一般平行四边形不具有的性质是　　　　　　　　　　　　　　　　　(　　　)
A.对角线相等　　　
　B.对边相等
C.对角相等　　　　
　D.对角线互相平分

答案： A

3.如图,在矩形ABCD中,AB = 24,BC = 25，以点B为圆心，BC的长为半径画弧，交边AD于点E,则EC的长为　　　　　(　　　)


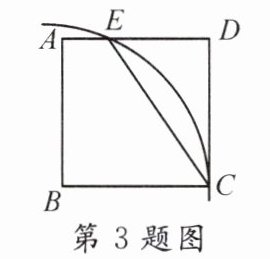
A.26　　　
　B.28　　
　C.30　　
　D.32

答案： C

4.如图，矩形ABCD的顶点A、C分别在直线a、b上,且a//b,若∠1 = 60°,则∠2的度数为(　　　)


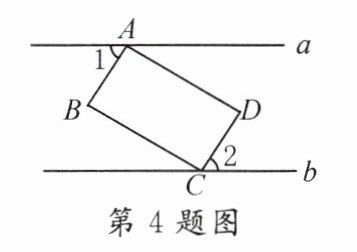
A.30°　　
　B.45°　
　C.60°　
　D.75°

答案： C

5.如图，在矩形ABCD中，∠ABC的平分线交AD于点E,连结CE.若BC = 7，AE = 4,则CE = ______.

答案： 5

6.如图，在矩形ABCD中,E是AB的中点，连结DE、CE.
(1)求证:△ADE≌△BCE.
(2)若AB = 6,AD = 4,求△CDE的周长.

答案：
(1)证明:
∵四边形ABCD是矩形，
∴AD = BC，∠A = ∠B = 90°.
∵E是AB的中点，
∴AE = BE.
∴△ADE≌△BCE.
(2)解:
∵△ADE≌△BCE，
∴DE = CE.在Rt△ADE中，
AD = 4，AE = $\frac{1}{2}$AB = 3，由勾股定理，得DE = $\sqrt{AD^{2}+AE^{2}}$ = $\sqrt{4^{2}+3^{2}}$ = 5.在矩形ABCD中，AB = CD，
∴DE + CE + CD = 2DE + AB = 2×5 + 6 = 16，即△CDE的周长为16.

7.如图,在矩形ABCD中,连结对角线AC、BD,将△ABC沿BC方向平移，使点B移到点C,得到△DCE.
(1)求证:△ACD≌△EDC.
(2)请探究△BDE的形状,并说明理由.

答案：
(1)证明:
∵四边形ABCD是矩形，
∴AD = CB，CD = AB.又
∵AC = CA，
∴△ACD≌△CAB.由平移的性质，得△CAB≌△EDC.
∴△ACD≌△EDC.
(2)解:△BDE是等腰三角形.理由如下:
∵AC = BD，DE = AC，
∴BD = DE.
∴△BDE是等腰三角形.