《2025年一线调研学业测评八年级数学下册华师大版》

11. 如图,在平面直角坐标系中,点B在y轴上,点C在反比例函数$y = -\frac{6}{x}$的图象上，则菱形OABC的面积为(　　　)
　
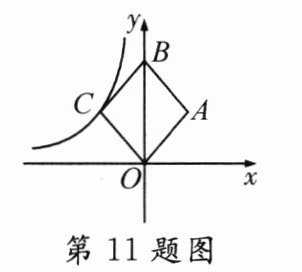
A. 12　　　B. 9　　　　C. 6　　　　D. 3
　　　

答案： A

12. 如图,已知菱形ABCD的一个内角∠BAD = 80°,对角线AC、BD相交于点O,点E在AB上,且BE = BO,则∠AOE = ________.

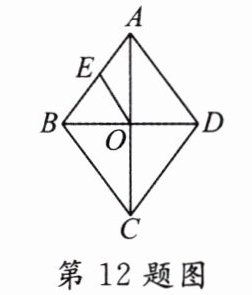
答案： 25°

13. 如图，菱形ABCD中,对角线AC = 6,BD = 8,M、
　　　　　　　　　　　　
N分别是BC、CD的中点,P是线段BD上的一个动点，则PM + PN的最小值是______.

答案： 5

14. 如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F.求证:DF = BE.

答案： 证明:连结AC。
∵四边形ABCD是菱形，
∴AC平分∠DAB，CD = CB。又
∵CF⊥AD，CE⊥AB，
∴CF = CE，∠CFD = ∠CEB = 90°。在Rt△CDF与Rt△CBE中，
$\begin{cases}CD = CB\\CF = CE\end{cases}$
∴Rt△CDF≌Rt△CBE(H.L.)。
∴DF = BE。

15. 如图，四边形ABCD是菱形，对角线AC，BD交于点O,E是边AD上一动点，过点E作EF⊥BD,EG⊥AC,点F,G为垂足，若AC = 10,BD = 24,求FG的最小值.
　　　　　　　　　　

答案： 解:连结OE。
∵四边形ABCD是菱形，AC = 10，BD = 24，
∴OA = OC = 5，OB = OD = 12，AC⊥BD。
在Rt△AOD中，$AD = \sqrt{AO^{2}+DO^{2}} = 13$。
∵EF⊥BD，EG⊥AC，AC⊥BD，
∴∠EFO = ∠EGO = ∠GOF = 90°，
∴四边形EFOG为矩形。
∴FG = OE。
当OE⊥AD时，OE取最小值，最小值为$\frac{AO\cdot OD}{AD}=\frac{60}{13}$，
∴FG的最小值为$\frac{60}{13}$。

16. 在菱形ABCD中,∠ABC = 60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF = AE,连结BE、EF.
　(1)如图1,当E是线段AC的中点时,求证:BE = EF.
　(2)如图2,当点E不是线段AC的中点，其他条件不变时，请你判断(1)中的结论是否成立？若成立，请证明;若不成立，说明理由.
　　　　

答案：

(1)证明:
∵四边形ABCD是菱形，
∴AB = BC。
∵∠ABC = 60°，
∴△ABC是等边三角形。
∴∠BCA = 60°。
∵E是线段AC的中点，
∴∠CBE = ∠ABE = 30°，AE = CE。
∵CF = AE，
∴CE = CF。
∴∠F = ∠CEF = $\frac{1}{2}$∠BCA = 30°。
∴∠CBE = ∠F = 30°。
∴BE = EF。
(2)解:
(1)中的结论仍然成立。证明如下:
如图，过点E作EG//BC交AB于点G。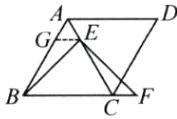
由
(1)，得△ABC是等边三角形，则AB = AC，∠BAC = ∠ACB = 60°。
∴∠ECF = 120°。
∵EG//BC，
∴∠AGE = ∠ABC = 60°。
又
∵∠BAC = 60°，
∴△AGE是等边三角形。
∴AG = AE = GE。
∴BG = EC，∠BGE = 120° = ∠ECF；又
∵CF = AE，
∴GE = CF。
∴△BGE≌△ECF。
∴BE = EF。