第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
11. 已知关于x的一次函数y = 3x + n的图象如图,则关于x的一次方程3x + n = 0的解是( )
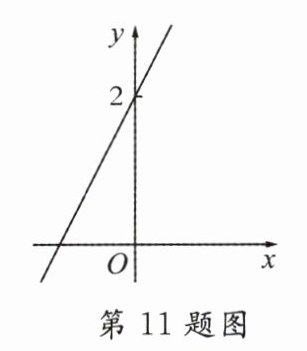
A. x = - 2
B. x = - 3
C. x = -$\frac{3}{2}$
D. x = -$\frac{2}{3}$

A. x = - 2
B. x = - 3
C. x = -$\frac{3}{2}$
D. x = -$\frac{2}{3}$
答案:
D
12. (鄂州中考)数形结合是解决数学问题常用的思想方法.如图,直线y = 2x - 1与直线y = kx + b(k≠0)相交于点P(2,3).根据图象可知,关于x的不等式2x - 1>kx + b的解集是 ( )
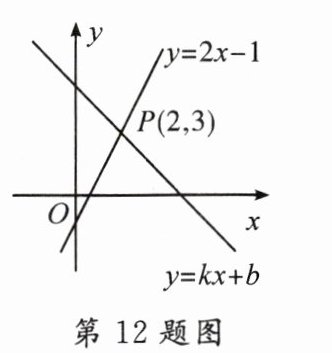
A. x<2
B. x<3
C. x>2
D. x>3

A. x<2
B. x<3
C. x>2
D. x>3
答案:
C
13. (福建中考)如图,一次函数y = kx + b(k>0)的图象过点( - 1,0),则不等式k(x - 1) + b>0的解集是 ( )
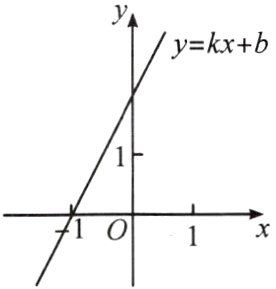
A. x> - 2
B. x> - 1
C. x>0
D. x>1

A. x> - 2
B. x> - 1
C. x>0
D. x>1
答案:
C
14. 如图,直线y = - 2x与直线y = kx + b相交于点A(a,2),并且直线y = kx + b经过点B(2,0).
(1) 求直线y = kx + b的表达式.
(2) 求两条直线与y轴围成的三角形的面积.
(3) 直接写出不等式(k + 2)x + b≥0的解集.
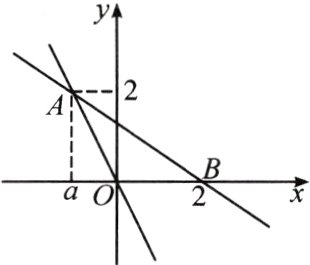
(1) 求直线y = kx + b的表达式.
(2) 求两条直线与y轴围成的三角形的面积.
(3) 直接写出不等式(k + 2)x + b≥0的解集.

答案:
解:
(1)把A(a,2)代入y=−2x,得−2a=2,即a=−1.
∴点A的坐标为(−1,2).把A(−1,2)、B(2,0)代入y=kx+b,得$\begin{cases}-k + b = 2 \\ 2k + b = 0 \end{cases}$,解得$\begin{cases} k = -\frac{2}{3} \\ b = \frac{4}{3} \end{cases}$.
∴所求直线的表达式是y=−$\frac{2}{3}$x+$\frac{4}{3}$.
(2)设直线AB与y轴交于点C,则点C的坐标为(0,$\frac{4}{3}$).
∴$S_{\triangle AOC}=\frac{1}{2}×\frac{4}{3}×1=\frac{2}{3}$.
(3)x≥−1.
(1)把A(a,2)代入y=−2x,得−2a=2,即a=−1.
∴点A的坐标为(−1,2).把A(−1,2)、B(2,0)代入y=kx+b,得$\begin{cases}-k + b = 2 \\ 2k + b = 0 \end{cases}$,解得$\begin{cases} k = -\frac{2}{3} \\ b = \frac{4}{3} \end{cases}$.
∴所求直线的表达式是y=−$\frac{2}{3}$x+$\frac{4}{3}$.
(2)设直线AB与y轴交于点C,则点C的坐标为(0,$\frac{4}{3}$).
∴$S_{\triangle AOC}=\frac{1}{2}×\frac{4}{3}×1=\frac{2}{3}$.
(3)x≥−1.
15. (黔西南州中考)甲、乙两家水果商店,平时以同样的价格出售品质相同的樱桃.春节期间,甲、乙两家商店都让利酬宾.甲商店的樱桃价格为60元/kg;乙商店的樱桃价格为65元/kg,若一次购买2kg以上,超过2kg部分的樱桃价格打8折.
(1) 设购买樱桃xkg,y甲、y乙(单位:元)分别表示顾客到甲、乙两家商店购买樱桃的付款金额,求y甲、y乙关于x的函数表达式.
(2) 春节期间,如何选择甲、乙两家商店购买樱桃更省钱?
(1) 设购买樱桃xkg,y甲、y乙(单位:元)分别表示顾客到甲、乙两家商店购买樱桃的付款金额,求y甲、y乙关于x的函数表达式.
(2) 春节期间,如何选择甲、乙两家商店购买樱桃更省钱?
答案:
解:
(1)由题意可得y甲关于x的函数表达式为y甲=60x.
当x≤2时,y乙=65x;
当x>2时,y乙=65×2+65×0.8(x−2)=52x+26.
∴y乙关于x的函数表达式为$y_{乙}=\begin{cases}65x(x\leq2) \\ 52x + 26(x\gt2) \end{cases}$.
(2)当60x<52x+26时,即x<$\frac{13}{4}$时,到甲商店购买樱桃更省钱;
当60x=52x+26时,即x=$\frac{13}{4}$时,到甲、乙两家商店购买樱桃花费相同;
当60x>52x+26,即x>$\frac{13}{4}$时,到乙商店购买樱桃更省钱.
(1)由题意可得y甲关于x的函数表达式为y甲=60x.
当x≤2时,y乙=65x;
当x>2时,y乙=65×2+65×0.8(x−2)=52x+26.
∴y乙关于x的函数表达式为$y_{乙}=\begin{cases}65x(x\leq2) \\ 52x + 26(x\gt2) \end{cases}$.
(2)当60x<52x+26时,即x<$\frac{13}{4}$时,到甲商店购买樱桃更省钱;
当60x=52x+26时,即x=$\frac{13}{4}$时,到甲、乙两家商店购买樱桃花费相同;
当60x>52x+26,即x>$\frac{13}{4}$时,到乙商店购买樱桃更省钱.
查看更多完整答案,请扫码查看


