《2025年一线调研学业测评八年级数学下册华师大版》

1. 一个正比例函数的图象经过点(−2,4)，它的表达式为　　　　　　　　　　　　(　　　)
A. y = −2x　　　　　　　
B. y = 2x
C. y = −$\frac{1}{2}$x　　　　　　　
D. y = $\frac{1}{2}$x

答案： A

2. 过点Q(0,4)的一次函数的图象与正比例函数y = 2x的图象相交于点P(1,k)，则这个一次函数的表达式为　　　　　　　　(　　　)
A. y = 2x + 4　　　　　　
B. y = −2x + 4
C. y = 2x − 4　　　　　　　
D. y = −2x − 4

答案： B

3. 一次函数y = kx + b的图象经过第四象限，与y轴交于点(0,3)，且它的图象与坐标轴围成的三角形面积为3，则k、b的值为　　(　　　)
A. k = −$\frac{3}{2}$, b = 3
B. k = $\frac{3}{2}$, b = 3
C. k = $\frac{3}{2}$, b = −3
D. k = $\frac{3}{2}$, b = 3或k = −$\frac{3}{2}$, b = 3

答案： A

4. 已知y是x的一次函数，下表给出了部分对应值，则m的值是________.

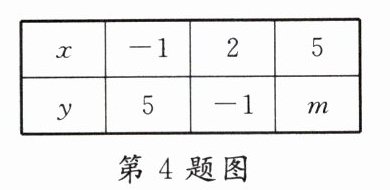
答案： −7

5. 如图，一次函数y = kx + b的图象与正比例函数y = 2x的图象平行且经过点A(1,−2)，则k − b =______.

答案： 6

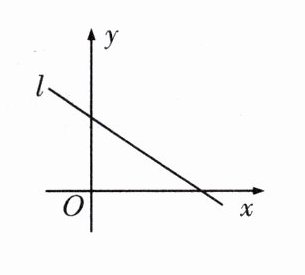
6. 如图，在平面直角坐标系中，直线l经过第一、二、四象限，点A(0,m)在l上.
(1)在图中标出点A.
(2)若m = 2，且l过点(−3,4)，求直线l的表达式.

答案： 解:
(1)图略.
(2)设直线l的表达式为y=kx+b.把(0,2)、(−3,4)分别代入，得$\begin{cases}b = 2 \\ -3k + b = 4\end{cases}$，解得$\begin{cases}k = -\frac{2}{3} \\ b = 2\end{cases}$。故直线l的表达式为$y = -\frac{2}{3}x + 2$。

7. 如图，已知一次函数的图象与x轴、y轴分别交于点A(−2,0)、B(0,3).
(1)直线AB的表达式为______________.
(2)过点B的另外一条直线l与x轴交于点C(c,0)，若点A、B、C构成面积不大于6的三角形，求c的取值范围.

答案： 解:
(1)$y = \frac{3}{2}x + 3$
(2)根据题意，得$\frac{1}{2}×3|c + 2| \leq 6$，且$c \neq -2$。解得$-6 \leq c \leq 2$，且$c \neq -2$。

8. (绍兴中考)I号无人机从海拔10m处出发，以10m/min的速度匀速上升，II号无人机从海拔30m处同时出发，以am/min的速度匀速上升，经过5min两架无人机位于同一海拔高度b(m).无人机海拔高度y(m)与时间x(min)的关系如图.两架无人机都上升了15min.
(1)求b的值及II号无人机海拔高度y(m)与时间x(min)的关系式.
(2)问当无人机上升了多长时间时，I号无人机比II号无人机高28米.

答案： 解:
(1)$b = 10 + 10×5 = 60$，
　设II号无人机海拔高度$y(m)$与时间$x(min)$的关系式为$y = kx + t$，
　将$(0,30)$、$(5,60)$代入上式，得$\begin{cases}t = 30 \\ 5k + t = 60\end{cases}$，解得$\begin{cases}k = 6 \\ t = 30\end{cases}$。
　故II号无人机海拔高度$y(m)$与时间$x(min)$的关系式为$y = 6x + 30(0 \leq x \leq 15)$。
(2)由题意得$(10x + 10) - (6x + 30) = 28$。
　解得$x = 12 \lt 15$。
　故当无人机上升了$12min$时，I号无人机比II号无人机高$28$米。