第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
10. 在▱ABCD中,AB = 7,AC = 6,则对角线BD的取值范围是( )
A. 8<BD<20
B. 6<BD<7
C. 4<BD<10
D. 1<BD<13
A. 8<BD<20
B. 6<BD<7
C. 4<BD<10
D. 1<BD<13
答案:
A [解析]令▱ABCD两对角线的交点为O,则BD = 2OB,OA = OC = 3.在△AOB中,
∵AB - OA < OB < AB + OA,
∴4 < OB < 10.
∴BD的取值范围是8 < BD < 20.
∵AB - OA < OB < AB + OA,
∴4 < OB < 10.
∴BD的取值范围是8 < BD < 20.
11. 如图,在▱ABCD中,AB = 5,∠BAD的平分线与DC交于点E,BF⊥AE,交AD的延长线于点F,则BC = ( )


答案:
B [解析]易证△AEF ≌ △AEB,则EF = EB,AF = AB = 5.易证△BCE ≌ △FDE,则BC = FD.在▱ABCD中,BC = AD,
∴FD = AD = $\frac{1}{2}$AB = 2.5.
∴BC = AD = 2.5.
∴FD = AD = $\frac{1}{2}$AB = 2.5.
∴BC = AD = 2.5.
12. 教材P78例6变式如图1,已知▱ABCD的对角线AC、BD相交于点O,EF过点O与直线AD、BC分别相交于点E、F。
(1)求证:AE = CF。
(2)将EF转动到图2的位置,EF与□ABCD的两条边DA、BC的延长线分别相交于点E、F,那么(1)中的结论是否成立?说明你的理由。
(3)若AD = 4,DE = 6,则CF = __________。

(1)求证:AE = CF。
(2)将EF转动到图2的位置,EF与□ABCD的两条边DA、BC的延长线分别相交于点E、F,那么(1)中的结论是否成立?说明你的理由。
(3)若AD = 4,DE = 6,则CF = __________。

答案:
(1)证明:
∵四边形ABCD是平行四边形,
∴AD // BC,OA = OC.
∴∠EAO = ∠FCO.又
∵∠EOA = ∠FOC,
∴△AOE ≌ △COF(A.S.A.).
∴AE = CF.
(2)解:
(1)中的结论成立.理由:同
(1)得△AOE ≌ △COF.
∴AE = CF.
(3)2或10
(1)证明:
∵四边形ABCD是平行四边形,
∴AD // BC,OA = OC.
∴∠EAO = ∠FCO.又
∵∠EOA = ∠FOC,
∴△AOE ≌ △COF(A.S.A.).
∴AE = CF.
(2)解:
(1)中的结论成立.理由:同
(1)得△AOE ≌ △COF.
∴AE = CF.
(3)2或10
13. 如图,在▱ABCD中,分别以BC、CD为边作等腰三角形BCF和等腰三角形CDE,使BC = BF,CD = DE,∠CBF = ∠CDE,连结AF、AE。
(1)求证:△ABF≌△EDA。
(2)延长AB与CF相交于点G。若AF⊥AE,求证:BF⊥BC。

(1)求证:△ABF≌△EDA。
(2)延长AB与CF相交于点G。若AF⊥AE,求证:BF⊥BC。

答案:
证明:
(1)
∵四边形ABCD是平行四边形,
∴AB = CD,AD = BC,∠ABC = ∠ADC.
∵BC = BF,CD = DE,
∴BF = DA,AB = ED.
∵∠ABF + ∠ABC + ∠CBF = 360°,∠EDA + ∠ADC + ∠CDE = 360°,∠CBF = ∠CDE,
∴∠ABF = ∠EDA.
∴△ABF ≌ △EDA(S.A.S.).
(2)如图,延长FB交AD于点H.
∵AF⊥AE,
∴∠EAF = 90°.
∵△ABF ≌ △EDA,
∴∠AFB = ∠EAD.
又
∵∠EAD + ∠FAH = 90°,
∴∠AFB + ∠FAH = 90°.
∴∠AHF = 90°,即BH⊥AD.
∵AD // BC,
∴BF⊥BC.
(1)
∵四边形ABCD是平行四边形,
∴AB = CD,AD = BC,∠ABC = ∠ADC.
∵BC = BF,CD = DE,
∴BF = DA,AB = ED.
∵∠ABF + ∠ABC + ∠CBF = 360°,∠EDA + ∠ADC + ∠CDE = 360°,∠CBF = ∠CDE,
∴∠ABF = ∠EDA.
∴△ABF ≌ △EDA(S.A.S.).
(2)如图,延长FB交AD于点H.
∵AF⊥AE,
∴∠EAF = 90°.
∵△ABF ≌ △EDA,
∴∠AFB = ∠EAD.
又
∵∠EAD + ∠FAH = 90°,
∴∠AFB + ∠FAH = 90°.
∴∠AHF = 90°,即BH⊥AD.
∵AD // BC,
∴BF⊥BC.
14. 如图,已知▱ABCD。
(1)试用三种不同的方法,用一条直线MN将它分成面积相等的两部分。(保留作图痕迹,不写作法)
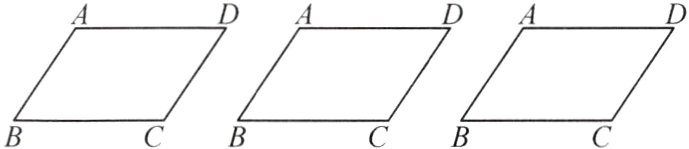
(2)由上述方法,你能得到什么一般性的结论?
(1)试用三种不同的方法,用一条直线MN将它分成面积相等的两部分。(保留作图痕迹,不写作法)

(2)由上述方法,你能得到什么一般性的结论?
答案:
解:
(1)直线MN如图所示.
(2)结论:过平行四边形对角线交点的任意一条直线都能将平行四边形分成面积相等的两部分.
(1)直线MN如图所示.
(2)结论:过平行四边形对角线交点的任意一条直线都能将平行四边形分成面积相等的两部分.
查看更多完整答案,请扫码查看


