第98页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
1 若存在一个整数m,使得关于x,y的方程组$\begin{cases}3x + 2y = 4m + 5,\\x - y = m - 1\end{cases}$的解满足$x + 4y\leqslant3$,且让不等式组$\begin{cases}5x - m>0,\\x - 4<-1\end{cases}$只有3个整数解,则满足条件的所有整数m的和是( ).
A. 12 B. 6 C. -10 D. -14
A. 12 B. 6 C. -10 D. -14
答案:
D
2 已知关于x,y的方程组$\begin{cases}x + y = - 7 - k,\\x - y = 1 + 3k\end{cases}$的解x为负数,y为非正数,求k的取值范围.
答案:
2. $\begin{cases}x + y = -7 - k,①\\x - y = 1 + 3k,②\end{cases}$ ①+②,得$2x = 2k - 6$,所以$x = k - 3$, ①-②,得$2y = -8 - 4k$,所以$y = -4 - 2k$。 由题意,得$\begin{cases}k - 3 < 0\\-4 - 2k \leq 0\end{cases}$,解得$-2 \leq k < 3$。
3 已知关于x,y的二元一次方程组$\begin{cases}3x + y = k + 1,\\x + 3y = 3.\end{cases}$
(1)若方程组的解x,y互为相反数,求k的值;
(2)若方程组的解x,y满足$\begin{cases}x + y<3,\\x - y>1,\end{cases}$求k的取值范围.
(1)若方程组的解x,y互为相反数,求k的值;
(2)若方程组的解x,y满足$\begin{cases}x + y<3,\\x - y>1,\end{cases}$求k的取值范围.
答案:
3.
(1)将两个方程相加,得$4x + 4y = k + 4$。 因为$x$,$y$互为相反数,所以$x + y = 0$, 则$4x + 4y = 0$,所以$k + 4 = 0$,解得$k = -4$。 故$k$的值为-4。
(2)将两个方程相减,得$2x - 2y = k - 2$, 所以$x - y = \frac{k - 2}{2}$。由
(1)得,$x + y = \frac{k + 4}{4}$, 所以$\begin{cases}\frac{k + 4}{4} < 3\\\frac{k - 2}{2} > 1\end{cases}$,解得$4 < k < 8$。 故$k$的取值范围为$4 < k < 8$。
(1)将两个方程相加,得$4x + 4y = k + 4$。 因为$x$,$y$互为相反数,所以$x + y = 0$, 则$4x + 4y = 0$,所以$k + 4 = 0$,解得$k = -4$。 故$k$的值为-4。
(2)将两个方程相减,得$2x - 2y = k - 2$, 所以$x - y = \frac{k - 2}{2}$。由
(1)得,$x + y = \frac{k + 4}{4}$, 所以$\begin{cases}\frac{k + 4}{4} < 3\\\frac{k - 2}{2} > 1\end{cases}$,解得$4 < k < 8$。 故$k$的取值范围为$4 < k < 8$。
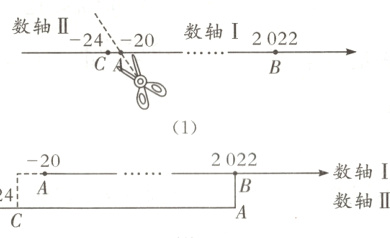
4 北京冬季奥运会开幕式在国家体育馆举行,嘉淇利用相关数字做游戏:
①画一条数轴,在数轴上用点A,B,C分别表示 - 20,2022, - 24,如图(1)所示;
②将这条数轴在点A处剪断,点A右侧的部分称为数轴Ⅰ,点A左侧的部分称为数轴Ⅱ;
③平移数轴Ⅱ使点A位于点B的正下方,如图(2)所示;
④扩大数轴Ⅱ的单位长度至原来的k倍,使点C正上方位于数轴Ⅰ的点A左侧.
则整数k的最小值为( ).
A. 511
B. 510
C. 509
D. 500
①画一条数轴,在数轴上用点A,B,C分别表示 - 20,2022, - 24,如图(1)所示;
②将这条数轴在点A处剪断,点A右侧的部分称为数轴Ⅰ,点A左侧的部分称为数轴Ⅱ;
③平移数轴Ⅱ使点A位于点B的正下方,如图(2)所示;
④扩大数轴Ⅱ的单位长度至原来的k倍,使点C正上方位于数轴Ⅰ的点A左侧.
则整数k的最小值为( ).

A. 511
B. 510
C. 509
D. 500
答案:
A
5 新情境 购买演唱会门票 (2024·江苏镇江丹徒区期末)
2024年4月,某歌手镇江演唱会在镇江体育会展中心举办,不同座位的票价不同,具体票价如下:
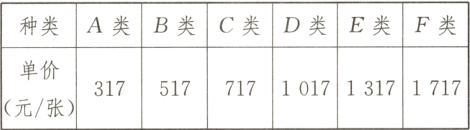
(1)小红爸爸购买了A类门票和B类门票共5张,总票价为1985元,A,B两类门票各买了多少张?
(2)小明妈妈购买了C类门票和D类门票共10张,且总票价不超过7770元,最少购买C类门票多少张?
2024年4月,某歌手镇江演唱会在镇江体育会展中心举办,不同座位的票价不同,具体票价如下:

(1)小红爸爸购买了A类门票和B类门票共5张,总票价为1985元,A,B两类门票各买了多少张?
(2)小明妈妈购买了C类门票和D类门票共10张,且总票价不超过7770元,最少购买C类门票多少张?
答案:
(1)设$A$类门票买了$x$张,$B$类门票买了$y$张,
根据题意,得$\begin{cases}x + y = 5\\317x + 517y = 1985\end{cases}$,解得$\begin{cases}x = 3\\y = 2\end{cases}$。
故$A$类门票买了3张,$B$类门票买了2张。
(2)设购买$C$类门票$m$张,则购买$D$类门票$(10 - m)$张,
根据题意,得$717m + 1017(10 - m) \leq 7770$,
解得$m \geq 8$,$\therefore m$的最小值为8。
故最少购买$C$类门票8张。
(1)设$A$类门票买了$x$张,$B$类门票买了$y$张,
根据题意,得$\begin{cases}x + y = 5\\317x + 517y = 1985\end{cases}$,解得$\begin{cases}x = 3\\y = 2\end{cases}$。
故$A$类门票买了3张,$B$类门票买了2张。
(2)设购买$C$类门票$m$张,则购买$D$类门票$(10 - m)$张,
根据题意,得$717m + 1017(10 - m) \leq 7770$,
解得$m \geq 8$,$\therefore m$的最小值为8。
故最少购买$C$类门票8张。
查看更多完整答案,请扫码查看


