《2025年1课3练江苏人民出版社七年级数学下册人教版》

9 (2024·贵阳一模)如图所示为两个形状、大小完全一样的小长方形拼接而成的图形.已知AB=5，CD=3，则此图形的面积为( ).

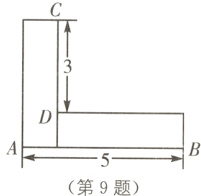
A. 6
B. 8
C. 10
D. 12

答案： B [解析]设小长方形的长为$x$，宽为$y$，由题意，得$\begin{cases}x + y = 5\\x - y = 3\end{cases}$，解得$\begin{cases}x = 4\\y = 1\end{cases}$.
$\therefore2xy = 8$，即此图形的面积为8. 故选B.

10 (2024·武汉江汉区一模)李老师将碗叠成一列(如图)，测量后发现：用2只碗叠放时总高度为7.5 cm，用4只碗叠放时总高度为11.5 cm.若将8个碗叠成一列正好能放入消毒柜，则这个消毒柜的高度至少有( ).

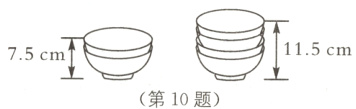
A. 15.5 cm
B. 19.5 cm
C. 23 cm
D. 30 cm

答案： B

11 (2024·河南新乡期末)汽车运输公司有A，B两种车型的旅游大客车，已知两种车型的座位数不同，1辆A型车和1辆B型车可乘坐105人，2辆A型车和1辆B型车可乘坐150人，则A，B两种车型大客车的座位数分别为( ).
A. 45，60
B. 65，45
C. 40，65
D. 60，45

答案： A

12 新情境 垃圾分类 (2024·无锡惠山区模拟)“践行垃圾分类·助力双碳目标”主题班会结束后，小乐和琪琪一起收集了一些废电池，小乐说：“我比你多收集了7节废电池.”琪琪说：“如果你给我8节废电池，我的废电池数量就是你的2倍.”如果他们说的都是真的，设小乐收集了x节废电池，琪琪收集了y节废电池，根据题意可列方程组为______.

答案： $\begin{cases}x - y = 7\\2(x - 8)=y + 8\end{cases}$

13 (2024·湖南长沙期中)如图，10块相同的长方形卡片拼成一个大长方形，设长方形卡片的长和宽分别为x和y，则依题意，列方程组为______.

(第13题)

答案： $\begin{cases}x + 2y = 75\\x = 3y\end{cases}$

14 (重庆实验外国语学校自主招生)河中有A，B两地相距210 km，两艘船分别从A，B两地同时出发，相向而行2小时相遇，朝一个方向行驶14时，甲追上乙，问甲的速度是______千米/小时.

答案： 60

15 新情境 组织研学活动 (2024·海南东方民族中学月考)“沉睡数千年，一醒惊天下”，三星堆遗址出土的文物再现了古蜀文明的辉煌景象.某校组织师生共480人开展三星堆博物馆研学活动.该校计划向运输公司租用A，B两种车型接送师生往返，若租用A型车3辆，B型车6辆，则空余15个座位；若租用A型车5辆，B型车4辆，则还有15人没有座位.
(1)求A，B两种车型各有多少个座位?
(2)若要求租用的每辆客车都坐满，那么共有多少种租车方案? 并列出所有的租车方案.

答案：
(1)设A型车有$x$个座位，B型车有$y$个座位，根据题意，得$\begin{cases}3x + 6y - 480 = 15\\5x + 4y + 15 = 480\end{cases}$，解得$\begin{cases}x = 45\\y = 60\end{cases}$.
故A型车有45个座位，B型车有60个座位.
(2)设租用A,B两种车型的辆数分别为$m$和$n$，根据题意，得$45m + 60n = 480$，则有$n=\frac{480 - 45m}{60}=8-\frac{3}{4}m$.
$\because m$，$n$均为非负整数，
$\therefore$当$m = 4$时，$n = 8-\frac{3}{4}\times4 = 5$，
当$m = 8$时，$n = 8-\frac{3}{4}\times8 = 2$.
所以共有2种租车方案:①租用A型车4辆，B型车5辆;②租用A型车8辆,B型车2辆.