第7页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
8 跨学科 光的反射 (2024·广东中山期末)如图是光的反射规律示意图. CO是入射光线,OD是反射光线,法线EO⊥AB,∠EOD = ∠COE. 若∠BOD = ∠COD,则∠AOC的度数为( ).
A. 30° B. 40° C. 45° D. 60°
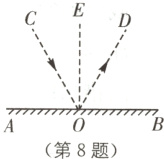
A. 30° B. 40° C. 45° D. 60°

答案:
D
9 (2024·安徽黄山期中)如图,直线AB,CD相交于点O,OM⊥AB.
(1)若∠1 = ∠2,求∠NOD的度数;
(2)若∠1 = $\frac{1}{5}$∠DOM,求∠AOC的度数.
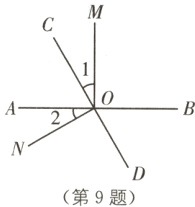
(1)若∠1 = ∠2,求∠NOD的度数;
(2)若∠1 = $\frac{1}{5}$∠DOM,求∠AOC的度数.

答案:
(1)
∵OM⊥AB,
∴∠AOM = 90°,
∴∠AOC + ∠1 = 90°.
∵∠1 = ∠2,
∴∠AOC + ∠2 = 90°,
∴∠NOD = 180° - (∠AOC + ∠2) = 90°.
(2)
∵∠1 = $\frac{1}{5}$∠DOM,∠1 + ∠DOM = 180°,
∴∠1 = $\frac{1}{6}$×180° = 30°.
∵∠AOM = 90°,
∴∠AOC = ∠AOM - ∠1 = 60°.
(1)
∵OM⊥AB,
∴∠AOM = 90°,
∴∠AOC + ∠1 = 90°.
∵∠1 = ∠2,
∴∠AOC + ∠2 = 90°,
∴∠NOD = 180° - (∠AOC + ∠2) = 90°.
(2)
∵∠1 = $\frac{1}{5}$∠DOM,∠1 + ∠DOM = 180°,
∴∠1 = $\frac{1}{6}$×180° = 30°.
∵∠AOM = 90°,
∴∠AOC = ∠AOM - ∠1 = 60°.
10 如图,OA⊥OB,OC为射线,OM平分∠AOC,ON平分∠BOC.
(1)若∠BOC = 50°,求∠MON的度数.
(2)当∠BOC的大小发生变化时,∠MON的大小发生变化吗?若不发生变化,求出∠MON的度数;若发生变化,试说明理由.
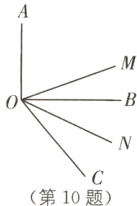
(1)若∠BOC = 50°,求∠MON的度数.
(2)当∠BOC的大小发生变化时,∠MON的大小发生变化吗?若不发生变化,求出∠MON的度数;若发生变化,试说明理由.

答案:
(1)∠MON = 45°.
(2)∠MON 的大小不变. 理由如下:
∵OA⊥OB,
∴∠AOB = 90°.
∵OM 平分∠AOC,ON 平分∠BOC,
∴∠COM = $\frac{1}{2}$∠AOC,∠CON = $\frac{1}{2}$∠BOC.
∴∠MON = ∠COM - ∠CON = $\frac{1}{2}$∠AOC - $\frac{1}{2}$∠BOC = $\frac{1}{2}$(∠AOC - ∠BOC) = $\frac{1}{2}$∠AOB = 45°.
故∠MON 的大小不变,为 45°.
(1)∠MON = 45°.
(2)∠MON 的大小不变. 理由如下:
∵OA⊥OB,
∴∠AOB = 90°.
∵OM 平分∠AOC,ON 平分∠BOC,
∴∠COM = $\frac{1}{2}$∠AOC,∠CON = $\frac{1}{2}$∠BOC.
∴∠MON = ∠COM - ∠CON = $\frac{1}{2}$∠AOC - $\frac{1}{2}$∠BOC = $\frac{1}{2}$(∠AOC - ∠BOC) = $\frac{1}{2}$∠AOB = 45°.
故∠MON 的大小不变,为 45°.
11 中考新考法 满足条件的结论开放 如图,直线AB,CD相交于点O,作∠DOE = ∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系;
(2)若∠AOC:∠AOD = 2:7,OG⊥OE,求∠GOF的度数.
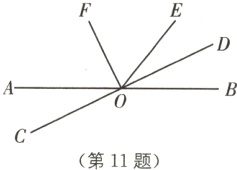
(1)判断OF与OD的位置关系;
(2)若∠AOC:∠AOD = 2:7,OG⊥OE,求∠GOF的度数.

答案:
(1)由 OF 平分∠AOE,得∠AOF = ∠EOF = $\frac{1}{2}$∠AOE.
由角的和差,得∠FOD = ∠FOE + ∠EOD = $\frac{1}{2}$∠AOE + $\frac{1}{2}$∠EOB = $\frac{1}{2}$(∠AOE + ∠EOB) = $\frac{1}{2}$∠AOB = 90°,
∴OF⊥OD.
(2)由∠AOC : ∠AOD = 2 : 7,得∠AOD = 3.5∠AOC.
由角的和差,得∠AOD + ∠AOC = 180°,
∴3.5∠AOC + ∠AOC = 180°,
∴∠AOC = 40°,
∴∠EOD = ∠BOD = ∠AOC = 40°.
由角的和差,得∠AOE = 180° - ∠AOC - ∠EOD = 180° - 40° - 40° = 100°.
由角平分线的性质,得∠EOF = $\frac{1}{2}$∠AOE = 50°.
∵OG⊥OE,
∴∠GOE = 90°.
当∠GOF 是锐角时,∠GOF = 90° - ∠EOF = 90° - 50° = 40°;
当∠GOF 是钝角时,∠GOF = 180° - 40° = 140°.
故∠GOF 的度数为 40°或 140°.
(1)由 OF 平分∠AOE,得∠AOF = ∠EOF = $\frac{1}{2}$∠AOE.
由角的和差,得∠FOD = ∠FOE + ∠EOD = $\frac{1}{2}$∠AOE + $\frac{1}{2}$∠EOB = $\frac{1}{2}$(∠AOE + ∠EOB) = $\frac{1}{2}$∠AOB = 90°,
∴OF⊥OD.
(2)由∠AOC : ∠AOD = 2 : 7,得∠AOD = 3.5∠AOC.
由角的和差,得∠AOD + ∠AOC = 180°,
∴3.5∠AOC + ∠AOC = 180°,
∴∠AOC = 40°,
∴∠EOD = ∠BOD = ∠AOC = 40°.
由角的和差,得∠AOE = 180° - ∠AOC - ∠EOD = 180° - 40° - 40° = 100°.
由角平分线的性质,得∠EOF = $\frac{1}{2}$∠AOE = 50°.
∵OG⊥OE,
∴∠GOE = 90°.
当∠GOF 是锐角时,∠GOF = 90° - ∠EOF = 90° - 50° = 40°;
当∠GOF 是钝角时,∠GOF = 180° - 40° = 140°.
故∠GOF 的度数为 40°或 140°.
12 中考新考法 类比猜想 如图,直线EF,CD相交于点O,OA⊥OB,且OC平分∠AOF.
(1)若∠AOE = 40°,求∠BOD的度数;
(2)若∠AOE = α,求∠BOD的度数;(用含α的式子表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?
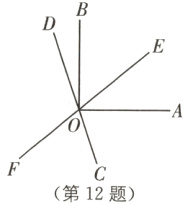
(1)若∠AOE = 40°,求∠BOD的度数;
(2)若∠AOE = α,求∠BOD的度数;(用含α的式子表示)
(3)从(1)(2)的结果中能看出∠AOE和∠BOD有何关系?

答案:
(1)
∵OA⊥OB,
∴∠AOB = 90°.
∴∠BOE = ∠AOB - ∠AOE = 50°.
∵∠AOE + ∠AOF = 180°,∠AOE = 40°,
∴∠AOF = 140°.
∵OC 平分∠AOF,
∴∠FOC = $\frac{1}{2}$∠AOF = 70°.
∴∠EOD = ∠FOC = 70°.
∴∠BOD = ∠EOD - ∠BOE = 20°.
(2)
∵OA⊥OB,
∴∠AOB = 90°.
∴∠BOE = ∠AOB - ∠AOE = 90° - α.
∵∠AOE + ∠AOF = 180°,∠AOE = α,
∴∠AOF = 180° - α.
又 OC 平分∠AOF,
∴∠FOC = $\frac{1}{2}$∠AOF = 90° - $\frac{1}{2}$α.
∴∠EOD = ∠FOC = 90° - $\frac{1}{2}$α.
∴∠BOD = ∠EOD - ∠BOE = $\frac{1}{2}$α.
(3)从
(1)
(2)的结果中能看出∠AOE = 2∠BOD.
(1)
∵OA⊥OB,
∴∠AOB = 90°.
∴∠BOE = ∠AOB - ∠AOE = 50°.
∵∠AOE + ∠AOF = 180°,∠AOE = 40°,
∴∠AOF = 140°.
∵OC 平分∠AOF,
∴∠FOC = $\frac{1}{2}$∠AOF = 70°.
∴∠EOD = ∠FOC = 70°.
∴∠BOD = ∠EOD - ∠BOE = 20°.
(2)
∵OA⊥OB,
∴∠AOB = 90°.
∴∠BOE = ∠AOB - ∠AOE = 90° - α.
∵∠AOE + ∠AOF = 180°,∠AOE = α,
∴∠AOF = 180° - α.
又 OC 平分∠AOF,
∴∠FOC = $\frac{1}{2}$∠AOF = 90° - $\frac{1}{2}$α.
∴∠EOD = ∠FOC = 90° - $\frac{1}{2}$α.
∴∠BOD = ∠EOD - ∠BOE = $\frac{1}{2}$α.
(3)从
(1)
(2)的结果中能看出∠AOE = 2∠BOD.
查看更多完整答案,请扫码查看


