第76页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
1 (2024·江苏常州期末)老师利用两块大小一样的长方体木块测量一张桌子的高度,首先按照图(1)方式放置,再交换两木块的位置,按照图(2)方式放置,测量的数据如图,则桌子的高度是( )。

A. 77 cm B. 78 cm C. 79 cm D. 80 cm

A. 77 cm B. 78 cm C. 79 cm D. 80 cm
答案:
B
2 (2024·辽宁大连期中)如图,小强和小红一起搭积木,小强所搭的小塔高度为28厘米,小红所搭的小树高度为27厘米,设每块A型积木的高为x厘米,每块B型积木的高为y厘米,那么x+y=______厘米。
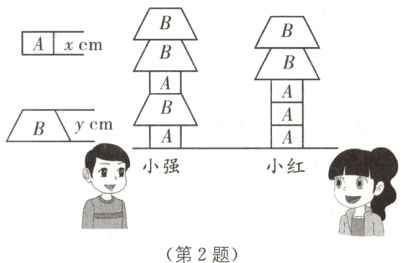

答案:
11
3 根据图中所给的信息,求出每个篮球和每个羽毛球的价格。
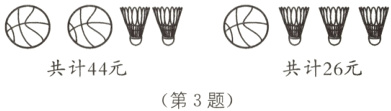

答案:
设每个篮球x元,每个羽毛球y元.
依题意,得$\begin{cases}2x + 2y = 44 \\x + 3y = 26 \end{cases}$,解得$\begin{cases}x = 20 \\y = 2 \end{cases}$.
故每个篮球20元,每个羽毛球2元.
依题意,得$\begin{cases}2x + 2y = 44 \\x + 3y = 26 \end{cases}$,解得$\begin{cases}x = 20 \\y = 2 \end{cases}$.
故每个篮球20元,每个羽毛球2元.
4 某电子超市销售甲、乙两种型号的蓝牙音箱,每台进价分别为240元,140元,下表是近两周的销售情况:(销售收入=销售单价×销售数量)
|销售时段|销售数量|销售收入|
|----|----|----|
| |甲种型号|乙种型号|
|第一周|3台|7台|2160元|
|第二周|5台|14台|4020元|
求甲、乙两种型号蓝牙音箱的销售单价。
|销售时段|销售数量|销售收入|
|----|----|----|
| |甲种型号|乙种型号|
|第一周|3台|7台|2160元|
|第二周|5台|14台|4020元|
求甲、乙两种型号蓝牙音箱的销售单价。
答案:
设甲种型号蓝牙音箱的销售单价为x元,乙种型号蓝牙音箱的销售单价为y元.
依题意,得$\begin{cases}3x + 7y = 2160 \\5x + 14y = 4020 \end{cases}$,解得$\begin{cases}x = 300 \\y = 180 \end{cases}$.
故甲种型号蓝牙音箱的销售单价为300元,乙种型号蓝牙音箱的销售单价为180元.
依题意,得$\begin{cases}3x + 7y = 2160 \\5x + 14y = 4020 \end{cases}$,解得$\begin{cases}x = 300 \\y = 180 \end{cases}$.
故甲种型号蓝牙音箱的销售单价为300元,乙种型号蓝牙音箱的销售单价为180元.
5 学校捐资购买了120吨物资打算支援山区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
|车型|甲|乙|丙|
|----|----|----|----|
|汽车运载量/(吨/辆)|5|8|10|
|汽车运费/(元/辆)|400|500|600|
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问:分别需甲、乙两种车型各几辆?
(2)为了节省运费,该公司打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14,你能分别求出三种车型的辆数吗? 此时的运费又是多少元?
|车型|甲|乙|丙|
|----|----|----|----|
|汽车运载量/(吨/辆)|5|8|10|
|汽车运费/(元/辆)|400|500|600|
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问:分别需甲、乙两种车型各几辆?
(2)为了节省运费,该公司打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14,你能分别求出三种车型的辆数吗? 此时的运费又是多少元?
答案:
(1)设需甲种车型x辆,乙种车型y辆,
根据题意,得$\begin{cases}5x + 8y = 120 \\400x + 500y = 8200 \end{cases}$,解得$\begin{cases}x = 8 \\y = 10 \end{cases}$.故需甲种车型8辆,乙种车型10辆.
(2)设甲种车型有a辆,乙种车型有b辆,则丙种车型有(14−a−b)辆,
由题意,得5a + 8b + 10(14−a−b)=120,
化简,得5a + 2b = 20,即$a = 4 - \frac{2}{5}b$.
因为a,b,14−a−b均为正整数,
所以b只能等于5,从而a = 2,14−a−b = 7,
所以甲种车型有2辆,乙种车型有5辆,丙种车型有7辆,
所以需运费400×2 + 500×5 + 600×7 = 7500(元).故甲种车型有2辆,乙种车型有5辆,丙种车型有7辆,需运费7500元.
(1)设需甲种车型x辆,乙种车型y辆,
根据题意,得$\begin{cases}5x + 8y = 120 \\400x + 500y = 8200 \end{cases}$,解得$\begin{cases}x = 8 \\y = 10 \end{cases}$.故需甲种车型8辆,乙种车型10辆.
(2)设甲种车型有a辆,乙种车型有b辆,则丙种车型有(14−a−b)辆,
由题意,得5a + 8b + 10(14−a−b)=120,
化简,得5a + 2b = 20,即$a = 4 - \frac{2}{5}b$.
因为a,b,14−a−b均为正整数,
所以b只能等于5,从而a = 2,14−a−b = 7,
所以甲种车型有2辆,乙种车型有5辆,丙种车型有7辆,
所以需运费400×2 + 500×5 + 600×7 = 7500(元).故甲种车型有2辆,乙种车型有5辆,丙种车型有7辆,需运费7500元.
查看更多完整答案,请扫码查看


