《2025年1课3练江苏人民出版社七年级数学下册人教版》

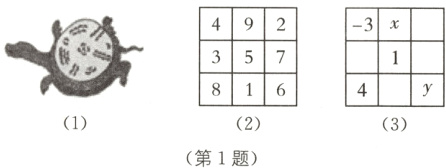
1 传统文化 洛书 教材P103练习T2·变式(2024·河北保定满城区期中)在大禹治水的时代，有一种神龟背负着一张神秘的图(如图(1))浮出洛水，吉祥献瑞，后世称之为“洛书”，当后人将“洛书”上的数填在图(2)的表中时发现：每行、每列、每条对角线上的三个数字之和相等，像这样的数字方阵，称为“幻方”，如果图(3)也是一个“幻方”，则x+y的值为( ).

A. 7
B. 9
C. 13
D. 15

答案： C

2 (2024·山西太原期中)某两位数，两个数位上的数之和为11.这个两位数加上45，得到的两位数恰好等于原两位数的两个数字交换位置所表示的数，求原两位数.
(1)列一元一次方程求解；
(2)设原两位数的十位数字为x，个位数字为y，列二元一次方程组；
(3)检验(1)中求得的结果是否满足(2)中的方程组.

答案：
(1)设原两位数的个位数字为m，则十位数字为(11 - m)，由题意，得10×(11 - m)+m + 45 = 10m+(11 - m)，解得m = 8，
∴11 - m = 3.
故原两位数为38.
(2)设原两位数的十位数字为x，个位数字为y，由题意，得$\begin{cases}x + y = 11\\10x + y + 45 = 10y + x\end{cases}$
(3)结合
(1)，可知x = 3，y = 8，
∴x + y = 11，10x + y + 45 = 83 = 10y + x，
∴
(1)中求得的结果满足
(2)中的方程组.
本题考查了一元一次方程的应用以及由实际问题抽象出二元一次方程组，解题的关键是：
(1)找准等量关系，正确列出一元一次方程；
(2)找准等量关系，正确列出二元一次方程组；
(3)将
(1)的结果代入方程组中验证方程组是否正确.

3 教材P106习题T8·变式(2024·天津河北区期末)某商场按定价销售某种商品时，每件可获利45元；按定价的8.5折销售该商品8件与将定价降低35元销售该商品12件所获利润相等.该商品的进价、定价分别是( ).
A. 95元，180元
B. 155元，200元
C. 100元，120元
D. 150元，125元

答案： B

4 (2024·海南中考)端午节是中国传统节日，人们有吃粽子的习俗.某商店售卖某品牌瘦肉粽和五花肉粽.如图，请依据以下对话，求促销活动前每个瘦肉粽、五花肉粽的售价.

答案： 设促销活动前每个瘦肉粽、五花肉粽的售价分别为x元、y元，
由题意，得$\begin{cases}(10x + 5y)×0.8 = 160\\x - y = 5\end{cases}$，解得$\begin{cases}x = 15\\y = 10\end{cases}$
故促销活动前每个瘦肉粽、五花肉粽的售价分别为15元，10元.

5 教材P101练习T1·拓展(2023·伊春中考)某社区为了打造“书香社区”，丰富小区居民的业余文化生活，计划出资500元全部用于采购A，B，C三种图书，A种每本30元，B种每本25元，C种每本20元，其中A种图书至少买5本，最多买6本(三种图书都要买)，此次采购的方案有( ).
A. 5种
B. 6种
C. 7种
D. 8种

答案： B

6 教材P104练习T1·拓展(2024·陕西西安三中期末)已知用2辆A型车和1辆B型车装满货物一次可运货10吨；用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有31吨货物，计划同时租用A型车a辆，B型车b辆，一次运完，且恰好每辆车都装满货物.
根据以上信息，解答下列问题：
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案(即A，B两种型号的车各租几辆，有几种租车方案).

答案：
(1)设1辆A型车和1辆B型车都装满货物一次可分别运货x吨，y吨，
根据题意，得$\begin{cases}2x + y = 10\\x + 2y = 11\end{cases}$，解得$\begin{cases}x = 3\\y = 4\end{cases}$
故1辆A型车和1辆B型车都装满货物一次可分别运货3吨，4吨.
(2)由题意，得3a + 4b = 31，
∴$b=\frac{31 - 3a}{4}$.
∵a，b均为整数，
∴有$\begin{cases}a = 1\\b = 7\end{cases}$，$\begin{cases}a = 5\\b = 4\end{cases}$和$\begin{cases}a = 9\\b = 1\end{cases}$三种情况.
故共有三种租车方案，分别为
①A型车1辆，B型车7辆；
②A型车5辆，B型车4辆；
③A型车9辆，B型车1辆.
本题考查了二元一次方程组的应用以及二元一次方程的应用，解题的关键是：
(1)根据等量关系，列出关于x，y的二元一次方程组，求解即可；
(2)由
(1)的结论结合共运货31吨，得出3a + 4b = 31，然后求出其正整数解即可.