《2025年1课3练江苏人民出版社七年级数学下册人教版》

1 教材P131思考·改编 下列式子中，是一元一次不等式的是( )．
A. $2x - 3$
B. $3 - x＞0$
C. $x - y = 3$
D. $x^{2}＞2$

答案： B

2 若$x^{m - 1}-1\geqslant2$是关于$x$的一元一次不等式，则$m =$________．

答案： 2

3 (2024·河北中考)下列数中，能使不等式$5x - 1＜6$成立的$x$的值为( )．
A. $1$
B. $2$
C. $3$
D. $4$

答案： A

4 教材P131例1·变式 (2024·长春南关区一模)不等式$2x - 2\leqslant0$的解集在数轴上表示正确的是( )．
　　

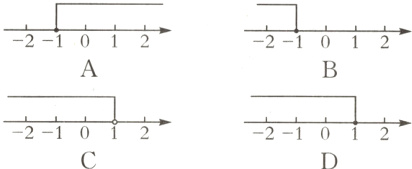
答案： D

5 (2024·河南新乡期末)一元一次不等式$7 - 3x\geqslant2x - 8$的非负整数解有( )．
A. $1$个
B. $2$个
C. $3$个
D. $4$个

答案： D

6 不等式$4(x + 1)＜16$的解集是________．

答案： $x＜3$

7 教材P137习题T4·变式 (2024·上海青浦区期末)不等式$5 - x＞2(x - 1)$的正整数解为________．

答案： 1,2

8 教材P132练习T1·变式 解下列不等式：
(1)$\frac{3x - 5}{2}＞2x$；
(2)$\frac{2 + x}{2}\geqslant\frac{2x - 1}{3}-1$；
(3)$\frac{3 - x}{2}＜1-\frac{x - 5}{4}$．

答案：
(1)$\frac{3x - 5}{2}＞2x$，去分母，得$3x - 5＞4x$，移项，得$3x - 4x＞5$，合并同类项，得$-x＞5$，系数化为1，得$x＜-5$；
(2)$\frac{2 + x}{2}\geqslant\frac{2x - 1}{3}-1$，去分母，得$3(2 + x)\geqslant2(2x - 1)-6$，去括号，得$6 + 3x\geqslant4x - 2 - 6$，移项，得$3x - 4x\geqslant-2 - 6 - 6$，合并同类项，得$-x\geqslant-14$，两边同时乘$-1$，得$x\leqslant14$；
(3)$\frac{3 - x}{2}＜1-\frac{x - 5}{4}$，去分母，得$2(3 - x)＜4-(x - 5)$，去括号，得$6 - 2x＜4 - x + 5$，移项，得$-2x + x＜4 + 5 - 6$，合并同类项，得$-x＜3$，系数化为1，得$x＞-3$

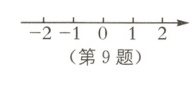
9 教材P136习题T1·拓展 (1)解不等式$2x - 1＞\frac{3x - 1}{2}$，并把它的解集在数轴上表示出来；
　　　　　　　　　　　　　　
(2)求不等式$\frac{3x + 2}{2}+1＞\frac{x + 9}{3}$的最小整数解．

答案：

(1)$2x - 1＞\frac{3x - 1}{2}$，去分母，得$4x - 2＞3x - 1$，移项，得$4x - 3x＞2 - 1$，合并同类项，得$x＞1$．将不等式的解集表示在数轴上如图: ；
(2)$\frac{3x + 2}{2}+1＞\frac{x + 9}{3}$，去分母，得$3(3x + 2)+6＞2(x + 9)$，去括号，得$9x + 6 + 6＞2x + 18$，移项，得$9x - 2x＞18 - 6 - 6$，合并同类项，得$7x＞6$，系数化为1，得$x＞\frac{6}{7}$．故最小整数解是1

10 (2024·陕西中考)不等式$2(x - 1)\geqslant6$的解集是( )．
A. $x\leqslant2$
B. $x\geqslant2$
C. $x\leqslant4$
D. $x\geqslant4$

答案： D

11 (2024·天津河北区期末)不等式$3-\frac{2x - 1}{3}\geqslant x$的非负整数解是________．

答案： 0,1,2

12 已知关于$x$的不等式$x - m\geqslant0$的负整数解只有$-1$，$-2$，$-3$，则$m$的取值范围是________．

答案： $-4＜m\leqslant-3$