《2025年1课3练江苏人民出版社七年级数学下册人教版》

1 教材P23练习T2·变式(2024·天津滨海新区期末)下列命题中是真命题的是( )．
A. 同位角相等
B. 三条直线两两相交，一定有三个交点
C. 过一点有且只有一条直线与已知直线垂直
D. 若a//b，b//c，则a//c

答案： D

2 下列说法不正确的是( )．
A. 基本事实一定是真命题
B. 假命题不是命题
C. 每个命题都有结论部分
D. 有些命题是错误的

答案： B

3 教材P24练习T2·改编(2024·天津和平区建华中学期末)有下列命题：①点到直线的距离是这一点到直线的垂线段；②两条直线被第三条直线所截，同旁内角相等；③在同一平面内，有且只有一条直线与已知直线垂直；④对顶角相等；⑤过一点有且只有一条直线与已知直线平行. 其中，真命题有( )．
A. 1个
B. 2个
C. 3个
D. 4个

答案： A

4 教材P23练习T3·改编(2024·天津滨海新区塘沽第二中学期末)将命题“在同一平面内，垂直于同一条直线的两条直线互相平行”改写为“如果……那么……”的形式，可写为________________.

答案： 如果在同一平面内，两条直线都垂直于同一条直线，那么这两条直线互相平行

5 (2024·宿迁中考改编)命题“两直线平行，同位角相等”改写成“如果……那么……”的形式是__________.

答案： 如果两直线平行，那么同位角相等

6 教材P24习题T2·改编下列推理中，错误的是( )．
A. ∵AB=CD，CD=EF，∴AB=EF
B. ∵∠α=∠β，∠β=∠γ，∴∠α=∠γ
C. ∵a//b，b//c，∴a//c
D. ∵AB⊥EF，EF⊥CD，∴AB⊥CD

答案： D

7 教材P23练习T2·变式 下列选项中，可以用来证明命题“若a＞b，则|a|＞|b|”是假命题的反例是( )．
A. a=1，b=-2
B. a=-1，b=2
C. a=-2，b=1
D. a=2，b=1

答案： A

8 中考新考法 满足结论的条件开放 以n=________为反例，可以证明命题“若n为自然数，则$2^n≥n^2”$为假命题.

答案： 3(答案不唯一)

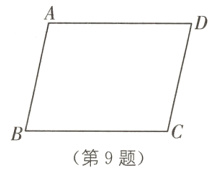
9 如图，在四边形ABCD中，①AB//CD，②∠A=∠C，③AD//BC.
(1)请你以其中两个为条件，第三个为结论，写出一个命题；
(2)判断这个命题是否为真命题，并说明理由.

答案：
(1)答案不唯一，如：如果AB//CD，∠A = ∠C，那么AD//BC.
(2)这个命题是真命题. 理由如下：
∵AB//CD，
∴∠B + ∠C = 180°.
∵∠A = ∠C，
∴∠B + ∠A = 180°，
∴AD//BC.
解后反思 已知三个条件，任意找出两个条件，一共有三种选择，本题无论怎么选择，组成的命题都是真命题.

10 如图，现有以下三句话：①AB//CD；②∠B=∠C；③∠E=∠F. 请以其中两句话为条件，第三句话为结论构造命题.
(1)你构造的是哪几个命题?
(2)你构造的命题是真命题还是假命题? 请加以证明.

答案：
(1)由①②得到③；由①③得到②；由②③得到①.
(2)由①②得到③为真命题. 证明如下：
∵AB//CD，
∴∠B = ∠CDF.
∵∠B = ∠C，
∴∠C = ∠CDF.
∴CE//BF.
∴∠E = ∠F.
由①③得到②为真命题. 证明如下：
∵AB//CD，
∴∠B = ∠CDF.
∵∠E = ∠F，
∴CE//BF.
∴∠C = ∠CDF.
∴∠B = ∠C.
由②③得到①为真命题. 证明如下：
∵∠E = ∠F，
∴CE//BF.
∴∠C = ∠CDF.
∵∠B = ∠C，
∴∠B = ∠CDF.
∴AB//CD.

11 给出下列四个命题：
①如果一个数的相反数等于它本身，那么这个数是0；②如果一个数的倒数等于它本身，那么这个数是1；③如果一个数的平方等于它本身，那么这个数是1或0；④如果一个数的绝对值等于它本身，那么这个数是正数. 其中假命题有( )．
A. 1个
B. 2个
C. 3个
D. 4个

答案： B