《2025年1课3练江苏人民出版社七年级数学下册人教版》

10 如图，直线a，b，c交于点O，若∠1 + ∠2 = 70°，则∠3的度数为(　　　)．

A. 35°
B. 70°
C. 100°
D. 110°

答案： D

11 (2023·河南中考)如图，直线AB，CD相交于点O，若∠1 = 80°，∠2 = 30°，则∠AOE的度数为(　　　)．

A. 30°
B. 50°
C. 60°
D. 80°

答案： B

12 (2024·辽宁盘锦期末)如图，直线AB与CD相交于点O，已知射线OE将∠AOD分成了两部分，若∠2 = 2∠1，∠1 = 36°，则∠3的度数是(　　　)．

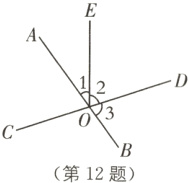
A. 36°
B. 56°
C. 60°
D. 72°

答案： D

13 (2024·天津河西区期末)如图，AB，CD相交于点O，OB平分∠DOE，若∠DOE = 100°，则∠AOE的度数为(　　　)．

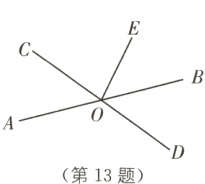
A. 100°
B. 110°
C. 120°
D. 130°

答案： D

14 中考新考法 满足条件的结论开放 如图，直线AB，CD相交于点O. 已知∠BOD = 75°，OE把∠AOC分成两个角，且∠AOE = $\frac{2}{3}$∠EOC，将射线OE绕点O逆时针旋转α(0° ＜ α ＜ 360°)到OF，当∠AOF = 120°时，α的度数是________．

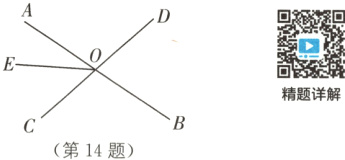
答案：
90°或210° [解析]①当OF运动到如图
(1)所示的位置时，
　
∵∠BOD=75°,
∴∠AOC=∠BOD=75°.
　
∵∠AOE=$\frac{2}{3}$∠EOC,
　
∴∠AOE=$\frac{2}{5}$∠AOC=$\frac{2}{5}$×75°=30°.
　　当∠AOF=120°时,α=∠AOF−∠AOE=120°−30°=90°;
　　 　　 (第14题)
　　②当OF运动到如图
(2)所示的位置时，
　
∵∠BOD=75°,
∴∠AOC=∠BOD=75°.
　
∵∠AOE=$\frac{2}{3}$∠EOC,
　
∴∠AOE=$\frac{2}{5}$∠AOC=$\frac{2}{5}$×75°=30°.
　　当∠AOF=120°时,α=360°−(∠AOF+∠AOE)=360°−150°=210°.
　　综上所述，α的度数是90°或210°.
归纳总结　　本题考查对顶角，根据比例求出角的度数以及角的和与差，掌握数形结合思想是解决问题的关键.

15 (2024·河南师大附中期中)如图，直线AB，CD相交于点O，OE把∠BOD分成两部分．
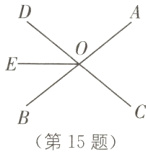
(1)直接写出图中∠AOD的对顶角为________，∠BOE的邻补角为________；
(2)若OE平分∠BOD，∠DOE：∠AOD = 1：4. 求∠EOC的度数．

答案：
(1)∠BOC ∠AOE
(2)设∠DOE = x，则∠AOD = 4x.
∵OE平分∠BOD，
∴∠BOE = ∠DOE = x，
∴x + x + 4x = 180°，解得x = 30°，
∴∠BOE = 30°，∠AOD = 4x = 120°，
∴∠BOC = ∠AOD = 120°，
∴∠EOC = ∠BOE + ∠BOC = 150°.
归纳总结 本题考查了几何图形中角的运算以及对顶角、邻补角、角平分线的定义，正确掌握相关性质是解题的关键.

16 中考新考法 规律探究 如图(1)，两条直线AB，CD相交于同一点O，所组成的角中，互为对顶角的有2对，∠AOD和∠COB，∠AOC和∠BOD.
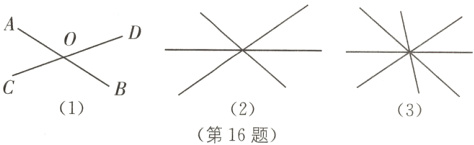
(1)如图(2)，三条直线相交于同一点所组成的角中，互为对顶角的有多少对?
(2)如图(3)，四条直线相交于同一点所组成的角中，互为对顶角的有多少对?
(3)n条直线相交于同一点所组成的角中，互为对顶角的有多少对?

答案：
(1)6对
(2)12对
(3)n(n - 1)对
归纳总结 本题考查了对顶角的定义，解题的关键是根据图形找出规律.