《2025年1课3练江苏人民出版社七年级数学下册人教版》

15 新情境 构建模型 (2024·山西太原期中)如图是游乐园一角的平面示意图，图中每个小方格的边长为1个单位长度，1个单位长度表示100 m.
(1)如果用有序数对(1,0)表示跳跳床的位置，用(-1,-2)表示大门的位置，则下面两个游乐设施的位置分别为：跷跷板______，碰碰车______；
(2)在(1)的条件下，秋千的位置是(3,2)，请在图中标出来；
(3)在(1)的条件下，旋转木马在大门以东400 m，再往北300 m处，请在图中标出来. (不必写坐标)
　　　　　　　　　　　　　　北
　　　 　　　　东
　　　　　　　　(第15题)

答案：

(1)(0,2) (3,-1) [解析]根据题意，建立平面直角坐标系如图所示.
所以跷跷板的位置可表示为(0,2)，碰碰车的位置可表示为(3,-1).
(2)秋千的位置如图所示.
(3)旋转木马的位置如图所示.

归纳总结 本题考查坐标确定位置，能根据所给点的坐标确定平面直角坐标系是解题的关键.

16 中考新考法 存在性问题探究 已知A(0,a)，B(0,b)，|5+a|+$\sqrt{4 - b}$=0，且点C在x轴的正半轴上，三角形ABC的面积为18.
(1)求a,b的值.
(2)求出点C的坐标.
(3)过点C作平行于y轴的直线，在该直线上是否存在一点D，使三角形BCD的面积是三角形ABC面积的$\frac{1}{3}$？若存在，请求出点D的坐标；若不存在，请说明理由.

答案：

(1)
∵|5 + a|+$\sqrt{4 - b}$=0，
∴5 + a=0，4 - b=0，
∴a=-5，b=4.
(2)如图
(1).
∵a=-5，b=4，
∴A(0,-5)，B(0,4)，
∴AB=9.
∵点C在x轴的正半轴上，
∴三角形ABC的面积=$\frac{1}{2}$AB·x_{C}=$\frac{1}{2}$×9x_{C}=18，
∴x_{C}=4，
∴C(4,0).

(3)如图
(2).
∵C(4,0)，CD//y轴，
∴设D(4,y).
∵三角形BCD的面积是三角形ABC面积的$\frac{1}{3}$，
∴三角形BCD的面积=$\frac{1}{2}$CD·x_{C}=$\frac{1}{2}$|y|·4=$\frac{1}{3}$×18=6，
∴|y|=3，
∴y=±3，
∴D(4,3)或D(4,-3).
解后反思 本题考查了坐标与图形，熟练掌握算术平方根和绝对值的非负性，利用数形结合的思想进行求解是解题的关键.

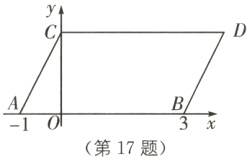
17 中考新考法 满足条件的结论开放 如图，在平面直角坐标系中，点A，B的坐标分别为(-1,0)，(3,0)，现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD.
(1)求点C，D的坐标及四边形ABDC的面积S四边形ABDC.
(2)在y轴上是否存在一点P，连接PA，PB，使S△PAB=S四边形ABDC？若存在，求出点P的坐标；若不存在，试说明理由.
　　　　　　　　　　

答案：
(1)由题意，得C(0,2)，D(4,2)，
S_{四边形ABDC}=AB×OC=4×2=8.
(2)在y轴上存在一点P，使S_{△PAB}=S_{四边形ABDC}.
理由如下：
设点P到AB的距离为h，
S_{△PAB}=$\frac{1}{2}$×AB×h=2h，
由S_{△PAB}=S_{四边形ABDC}，得2h=8，解得h=4，
∴P(0,4)或(0,-4).