《2025年1课3练江苏人民出版社七年级数学下册人教版》

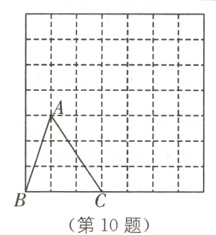
10 如图，在由边长为1个单位长度的小正方形组成的网格中，三角形ABC的顶点A，B，C在小正方形的顶点上，将△ABC向右平移3个单位长度，再向上平移2个单位长度得到三角形A₁B₁C₁.
(1)在网格中画出三角形A₁B₁C₁；
(2)三角形A₁B₁C₁的面积为________．

答案：

(1)如图，△A_{1}B_{1}C_{1}即为所求.

(2)$\frac{9}{2}$

11 如图，长方形ABCD的长为6，宽为4，将长方形先向上平移2个单位，再向右平移2个单位得到长方形A'B'C'D'，则阴影部分的面积是(　　　)．
　　　
A. 12
B. 10
C. 8
D. 6

答案： C

12 （2024·东营中考）如图，将△DEF沿FE方向平移3 cm得到△ABC，若△DEF的周长为24 cm，则四边形ABFD的周长为________cm.

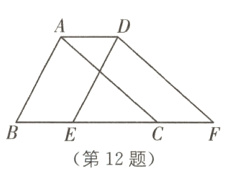
答案： 30 [解析]由平移的性质可知：AD = BE = 3 cm，AB = DE.
∵△DEF的周长为24 cm，
∴DE + EF + DF = 24 cm，
∴四边形ABFD的周长 = AB + BE + EF + DF + AD = 24 + 3 + 3 = 30(cm).

13 （2024·芜湖模拟）如图，相邻两线段互相垂直，甲、乙两人同时从点A处出发到点C处，甲沿着“A→B→C”的路线走，乙沿着“A→D→E→F→G→H→C”的路线走，若他们的行走速度相同，则甲、乙两人谁先到C处？________．

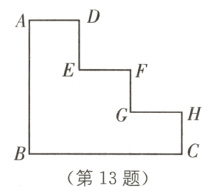
答案： 甲、乙两人同时到

14 （2024·天津河西区期末）如图，AB = 4 cm，BC = 5 cm，AC = 2 cm，将△ABC沿BC方向平移a cm(0＜a＜5)，得到△DEF，连接AD，则阴影部分的周长为________cm.

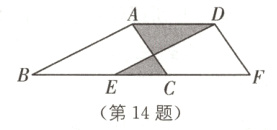
答案： 11

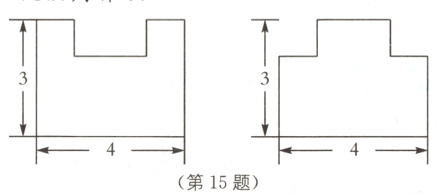
15 如图，根据图中给出的数据，判断第一个图形的周长L₁与第二个图形的周长L₂的关系：L₁________L₂.（填“等于”“大于”“小于”或“无法判断”）

答案：
大于 [解析]设凹槽的深度为a，如图，则第一个图形的周长$L_{1}=2×(3 + 4)+2a = 14 + 2a，$第二个图形的周长$L_{2}=2×(3 + 4)=14，$因此$L_{1}$大于$L_{2}.$

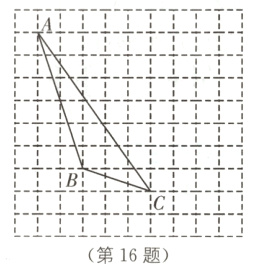
16 （2024·天津和平区建华中学期末）如图，在方格纸内将△ABC水平向右平移4个单位长度得到△A'B'C'. 利用网格点和直尺画图：
(1)画出△A'B'C'；
(2)画出AB边上的高线CD，图中△ABC的面积是________；
(3)△ABC与△EBC面积相等，在图中描出所有满足条件且异于A点的格点E，并记为E₁，E₂，E₃.

答案：

(1)如图
(1)，把点A，B，C分别向右平移4个单位长度得到点A′，B′，C′，再把点连接得到△A′B′C′，△A′B′C′即为所求.

(2)如图
(2)，延长AB，过点C作CD⊥AB于点D，CD即为所求.

8 [解析]由图可得，S_{△ABC}=$\frac{1}{2}$×5×7 - $\frac{1}{2}$×2×6 - 2×1 - $\frac{1}{2}$×1×3 = 8.
(3)如图
(3)，格点E_{1}，E_{2}，E_{3}即为所求.

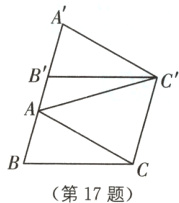
17 如图，将三角形ABC沿射线BA方向平移到三角形A'B'C'的位置，连接AC'.
(1)AA'与CC'的位置关系为________；
(2)求证：∠A'+∠CAC'+∠AC'C = 180°；
(3)设∠AC'B' = x，∠ACB = y，试探索∠CAC'与x，y之间的数量关系，并证明你的结论.

答案：

(1)AA′//CC′
(2)根据平移的性质可知A′C′//AC，AA′//CC′，
∴∠A′ = ∠BAC，∠BAC = ∠ACC′.
∴∠A′ = ∠ACC′.
∵∠ACC′ + ∠CAC′ + ∠AC′C = 180°，
∴∠A′ + ∠CAC′ + ∠AC′C = 180°.
(3)∠CAC′ = x + y. 理由如下：
如图，过点A作AD//BC，交CC′于点D，根据平移的性质可知B′C′//BC，
∴B′C′//AD//BC，
∴∠AC′B′ = ∠C′AD，∠ACB = ∠CAD，

∴∠CAC′ = ∠C′AD + ∠CAD = ∠AC′B′ + ∠ACB = x + y，即∠CAC′ = x + y.