《2025年1课3练江苏人民出版社七年级数学下册人教版》

10 如图，下列说法中错误的是(　　)。

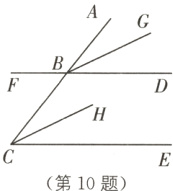
A. ∠GBD和∠HCE是同位角
B. ∠ABD和∠ACH是同位角
C. ∠FBC和∠ACE是内错角
D. ∠GBC和∠BCE是同旁内角

答案： A

11 如图，下列结论中正确的是(　　)。

A. ∠1和∠2是同位角
B. ∠2和∠3是同旁内角
C. ∠1和∠4是内错角
D. ∠3和∠4是对顶角

答案： B

12 (2024·北京怀柔区期末)如图，直线a，b被c所截，下列四个结论：①∠1和∠3互为对顶角；②∠4和∠8是同位角；③∠3和∠7是内错角；④∠4和∠7是同旁内角。其中，结论一定正确的有(　　)。

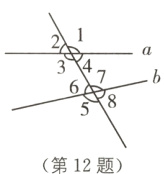
A. 4个
B. 3个
C. 2个
D. 1个

答案： A

13 (2024·广东广州期末)如图，有下列说法：①能与∠DEF构成内错角的角有2个；②能与∠BFE构成同位角的角有2个；③能与∠C构成同旁内角的角有4个。其中正确结论的序号是________。

答案： ①

14 跨学科 光的折射 如图，把一根筷子一端放在水里，一端露出水面，筷子变弯了？其实没有，这是光的折射现象，光从空气中射入水中，光的传播方向发生了改变。
(1)请指出∠1的同旁内角与∠2的内错角；
(2)若测得∠AOE=65°，∠BOM=145°，从水面上看斜插入水中的筷子，水下部分向上折弯了多少度？请说明理由。

答案：
(1)∠1 的同旁内角是∠MOE，∠AOE，∠ADE；∠2 的内错角是∠MOE，∠AOE.
(2)
∵∠BOM = 145°，
∴∠AOM = 180° - ∠BOM = 35°，
∴∠MOE = ∠AOE - ∠AOM = 65° - 35° = 30°，
∴水下部分向上折弯了 30 度.

15 新情境 构建模型 如图是一个跳棋棋盘，其游戏规则是：一个棋子从某一个起始角开始，经过若干步跳动以后，到达终点角。跳动时，每一步只能跳到它的同位角、内错角或同旁内角的位置上。例如：从起始位置∠1跳到终点位置∠3的路径有
路径1：∠1 $\xrightarrow{同旁内角}$ ∠9 $\xrightarrow{内错角}$ ∠3；
路径2：∠1 $\xrightarrow{内错角}$ ∠12 $\xrightarrow{内错角}$ ∠6 $\xrightarrow{同位角}$ ∠10 $\xrightarrow{同旁内角}$ ∠3；等。
(1)写出从∠1跳到∠8的一条路径；
(2)从起始位置∠1依次按同位角、内错角、同旁内角的顺序跳，能否跳到终点位置∠8？

答案：
(1)由题意，得从∠1 跳到∠8 的一条路径：∠1 $\xrightarrow{同旁内角}$∠9 $\xrightarrow{同位角}$∠7 $\xrightarrow{同旁内角}$∠8.(答案不唯一)
(2)能跳到终点位置∠8，路径为：∠1 $\xrightarrow{同位角}$∠10 $\xrightarrow{内错角}$∠5 $\xrightarrow{同旁内角}$∠8.