《2025年1课3练江苏人民出版社七年级数学下册人教版》

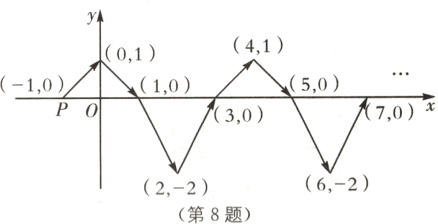
8 (2024.江西南昌期末)如图，在平面直角坐标系xOy中，动点P按图中箭头所示的方向依次运动，第1次从点(－1,0)运动到点(0,1)，第2次运动到点(1,0)，第3次运动到点(2,－2)，…，按这样的运动规律，动点P第2024次运动到点(　　　)。
A. （2023,0）
B. （2024,－2）
C. （2023,1）
D. （2024,0）
　　

答案： A

9 中考新考法 规律探究 (2024.山东中考)任取一个正整数，若是奇数，就将该数乘3再加上1；若是偶数，就将该数除以2. 反复进行上述两种运算，经过有限次运算后，必进入循环圈1→4→2→1，这就是“冰雹猜想”. 在平面直角坐标系xOy中，将点(x,y)中的x，y分别按照“冰雹猜想”同步进行运算得到新的点的横、纵坐标，其中x，y均为正整数. 例如，点(6,3)经过第1次运算得到点(3,10)，经过第2次运算得到点(10,5)，以此类推，则点(1,4)经过2024次运算后得到点________。

答案： (2,1)

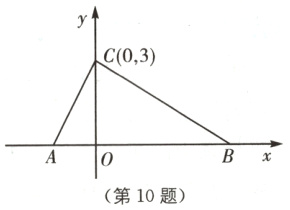
10 中考新考法 满足条件的结论开放 如图所示，在平面直角坐标系中，点A，B的坐标分别为A(a,0)，B(b,0)，且a，b满足|a＋2|＋$\sqrt{b - 4}$＝0，点C的坐标为(0,3)。
(1)求a，b的值及S△ABC；
(2)若点M在x轴上，且S△ACM＝$\frac{1}{3}$S△ABC，试求点M的坐标。
　　　　　　　　

答案：
(1)
∵$|a + 2|+\sqrt{b - 4}=0$，
∴$a + 2 = 0$，$b - 4 = 0$，
∴$a = - 2$，$b = 4$，
∴点 A 的坐标为(-2,0)，点 B 的坐标为(4,0)。
又点 C 的坐标为(0,3)，
∴$AB = | - 2 - 4| = 6$，$CO = 3$，
∴$S_{\triangle ABC}=\frac{1}{2}AB\cdot CO=\frac{1}{2}\times6\times3 = 9$。
(2)设点 M 的坐标为(x,0)，则$AM = |x - (-2)| = |x + 2|$，
又$S_{\triangle ACM}=\frac{1}{3}S_{\triangle ABC}$，
∴$\frac{1}{2}AM\cdot OC=\frac{1}{3}\times9$，
∴$\frac{1}{2}|x + 2|\times3 = 3$，
∴$|x + 2| = 2$，即$x + 2 = \pm2$，解得$x = 0$或 - 4。
故点 M 的坐标为(0,0)或(-4,0)。

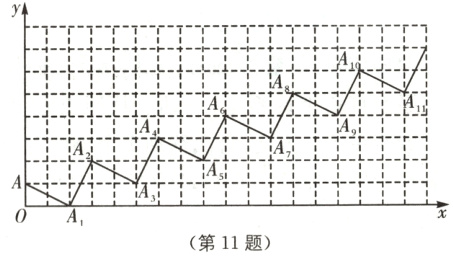
11 中考新考法 规律探究 (2024.天津和平区耀华中学期中改编)[观察发现]如图，观察下列各点的排列规律：A(0,1)，A₁(2,0)，A₂(3,2)，A₃(5,1)，A₄(6,3)，…。
[归纳应用]
(1)直接写出点A₆的坐标为________，点A₁₂的坐标为________；
(2)若点A₂n的坐标为(3036,1013)，求n的值。
　　

答案：
(1)(9,4) (18,7)
(2)
∵$A(0,1)$，$A_1(2,0)$，$A_2(3,2)$，$A_3(5,1)$，$A_4(6,3)$，且$A(0,1)$，$A_2(1\times3,1 + 1)$，$A_4(2\times3,1 + 2)$，$A_6(3\times3,1 + 3)$…，
以此类推，$A_{2n}(\frac{2n}{2}\times3,1+\frac{2n}{2})$，即$A_{2n}(3n,n + 1)$。
∵点$A_{2n}$的坐标为(3036,1013)，
∴$3n = 3036$，解得$n = 1012$。