《2025年昕金立文化单元金卷八年级数学上册人教版》

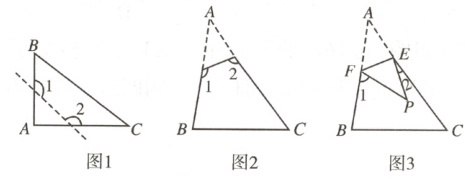
23.(11 分)(1)如图 1，△ABC 为直角三角形，∠A = 90°，若沿图中虚线剪去∠A，则∠1 + ∠2 = (C)
A.90°
B.135°
C.270°
D.315°
(2)如图 2，在△ABC 中，∠A = 40°，剪去∠A 后成为四边形，则∠1 + ∠2 =220°；
(3)如图 2，根据(1)与(2)的求解过程，请你归纳猜想∠1 + ∠2 与∠A 的关系：∠1 + ∠2 = 180° + ∠A；
(4)若没有剪掉∠A，而是把它折成如图 3 所示的形状，试探究∠1 + ∠2 与∠A 的关系，并说明理由.

答案： 23.解:
(1)C　
(2)220°　
(3)∠1 + ∠2 = 180° + ∠A
(4)∠1 + ∠2 = 2∠A.理由如下:
∵△EFP是由△EFA折叠得到的，
∴∠AFE = ∠PFE,∠AEF = ∠PEF,
∴∠1 = 180° - 2∠AFE,∠2 = 180° - 2∠AEF,
∴∠1 + ∠2 = 360° - 2(∠AFE + ∠AEF).又
∵∠AFE + ∠AEF = 180° - ∠A,
∴∠1 + ∠2 = 360° - 2(180° - ∠A) = 2∠A.