第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
11.(新乡期中)如图,在$\triangle ABC$中,$AD$平分$\angle BAC$交$BC$于点$D$,$\angle B = 60^{\circ}$,$\angle C = 26^{\circ}$.
(1)请用无刻度的直尺和圆规作出线段$AC$的垂直平分线;(保留作图痕迹)
(2)记(1)中所作$AC$的垂直平分线交$BC$于点$E$,交$AC$于点$F$,连接$AE$,求$\angle DAE$的度数.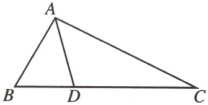
(1)请用无刻度的直尺和圆规作出线段$AC$的垂直平分线;(保留作图痕迹)
(2)记(1)中所作$AC$的垂直平分线交$BC$于点$E$,交$AC$于点$F$,连接$AE$,求$\angle DAE$的度数.

答案:
11.解:
(1)如图 所示,EF即为线段AC的垂直平分线.
所示,EF即为线段AC的垂直平分线.
(2)如图,
∵EF是AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C=26°.
又∠B=60°,
∴∠BAC=180°−26°−60°=94°.
∵AD平分∠BAC,
∴∠DAC=$\frac{1}{2}$∠BAC=47°,
∴∠DAE=∠DAC−∠EAC=21°.
11.解:
(1)如图
 所示,EF即为线段AC的垂直平分线.
所示,EF即为线段AC的垂直平分线.(2)如图,
∵EF是AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C=26°.
又∠B=60°,
∴∠BAC=180°−26°−60°=94°.
∵AD平分∠BAC,
∴∠DAC=$\frac{1}{2}$∠BAC=47°,
∴∠DAE=∠DAC−∠EAC=21°.
12.如图,每个小正方形的边长为$1$个单位长度,$\triangle ABC$中点$A$的坐标为$(-2,1)$,点$B$的坐标为$(-1,2)$.
(1)请在图中画出符合题意的平面直角坐标系,并写出点$C$的坐标_______;
(2)作出$\triangle ABC$关于$x$轴的对称图形$\triangle A_1B_1C_1$;
(3)若点$P(m,n)$在$\triangle ABC$的内部,当$\triangle ABC$沿$x$轴翻折后,点$P$的对应点$P_1$的坐标为_______.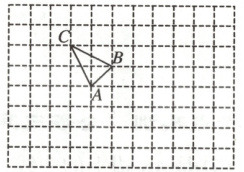
(1)请在图中画出符合题意的平面直角坐标系,并写出点$C$的坐标_______;
(2)作出$\triangle ABC$关于$x$轴的对称图形$\triangle A_1B_1C_1$;
(3)若点$P(m,n)$在$\triangle ABC$的内部,当$\triangle ABC$沿$x$轴翻折后,点$P$的对应点$P_1$的坐标为_______.

答案:
12.解:
(1)所作平面直角坐标系如图所示.(-3, 3)
(2)如图,△A₁B₁C₁即为所求.
(3)(m, -n)

12.解:
(1)所作平面直角坐标系如图所示.(-3, 3)
(2)如图,△A₁B₁C₁即为所求.
(3)(m, -n)

13.如图,四边形$ABCD$的对角线$AC$,$BD$相交于点$E$,若$\triangle ABC$是等边三角形,$AD \perp AB$,$AD = DC = 4$.
(1)求证:$BD$垂直平分$AC$;
(2)求$BE$的长.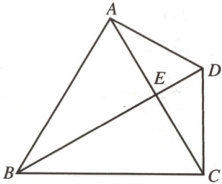
(1)求证:$BD$垂直平分$AC$;
(2)求$BE$的长.

答案:
13.
(1)证明:
∵AD=DC,
点D在线段AC的垂直平分线上.
∵△ABC是等边三角形,
∴BA=BC,
∴点B在线段AC的垂直平分线上,
∴BD是线段AC的垂直平分线,
∴BD垂直平分AC.
(2)解:
∵△ABC是等边三角形,AD⊥AB,BD垂直平分AC,
∴∠ABD=∠EAD=30°.
∵AD = DC = 4,
∴ BD = 8, ED = 2,
∴BE=BD−ED=8−2=6.
(1)证明:
∵AD=DC,
点D在线段AC的垂直平分线上.
∵△ABC是等边三角形,
∴BA=BC,
∴点B在线段AC的垂直平分线上,
∴BD是线段AC的垂直平分线,
∴BD垂直平分AC.
(2)解:
∵△ABC是等边三角形,AD⊥AB,BD垂直平分AC,
∴∠ABD=∠EAD=30°.
∵AD = DC = 4,
∴ BD = 8, ED = 2,
∴BE=BD−ED=8−2=6.
查看更多完整答案,请扫码查看


