第42页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
23.(11分)知识生成
通常情况下,用两种不同的方法计算同一图形的面积,可以得到
一个恒等式.
(1)如图1,根据图中阴影部分的面积可以得到的等式是
知识迁移
类似地,用两种不同的方法计算同一几何体的体积,也可以得到
一个恒等式.
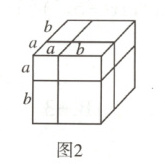
如图2是一个棱长为$a+b$的正方体,被分割成8块.
(2)用不同的方法计算这个正方体的体积,就可以得到一个等
式,这个等式为
(3)已知$a+b=3$,$ab=1$,利用上面的规律求$a^{3}+b^{3}$的值.

通常情况下,用两种不同的方法计算同一图形的面积,可以得到
一个恒等式.
(1)如图1,根据图中阴影部分的面积可以得到的等式是
$(a + b)^{2}-(a - b)^{2}=4ab$
.知识迁移
类似地,用两种不同的方法计算同一几何体的体积,也可以得到
一个恒等式.
如图2是一个棱长为$a+b$的正方体,被分割成8块.
(2)用不同的方法计算这个正方体的体积,就可以得到一个等
式,这个等式为
(3)已知$a+b=3$,$ab=1$,利用上面的规律求$a^{3}+b^{3}$的值.


答案:
23.解:
(1)$(a + b)^{2}-(a - b)^{2}=4ab$
(2)$(a + b)^{3}=a^{3}+3a^{2}b + 3ab^{2}+b^{3}$
(3)由
(2)可知$(a + b)^{3}=a^{3}+3a^{2}b + 3ab^{2}+b^{3}$,$\therefore a^{3}+b^{3}=(a + b)^{3}-3a^{2}b - 3ab^{2}=(a + b)^{3}-3ab(a + b)$.将$a + b = 3,ab = 1$代入,得$a^{3}+b^{3}=3^{3}-3×1×3 = 18$.
(1)$(a + b)^{2}-(a - b)^{2}=4ab$
(2)$(a + b)^{3}=a^{3}+3a^{2}b + 3ab^{2}+b^{3}$
(3)由
(2)可知$(a + b)^{3}=a^{3}+3a^{2}b + 3ab^{2}+b^{3}$,$\therefore a^{3}+b^{3}=(a + b)^{3}-3a^{2}b - 3ab^{2}=(a + b)^{3}-3ab(a + b)$.将$a + b = 3,ab = 1$代入,得$a^{3}+b^{3}=3^{3}-3×1×3 = 18$.
查看更多完整答案,请扫码查看


