第59页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
29.如图,在$3×3$的正方形网格中,格线的交点称为格点,以格点为顶点的三角形称为格点三角形,若图中的$\triangle ABC$为格点三角形,则在图中与$\triangle ABC$成轴对称的格点三角形可以画出
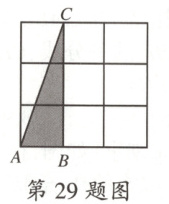
6
个.
答案:
29.6 [解析]分三种类型:
①对称轴为水平方向,有1个.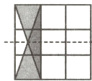
②对称轴为垂直方向,有3个.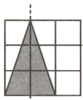
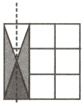
③对称轴为倾斜方向,有2个.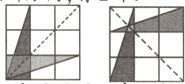
综上所述,满足条件的图形有6个.
29.6 [解析]分三种类型:
①对称轴为水平方向,有1个.

②对称轴为垂直方向,有3个.


③对称轴为倾斜方向,有2个.

综上所述,满足条件的图形有6个.
30.下列计算正确的是 (
A.$x^{3}· x^{4}=x^{12}$
B.$x^{8}÷ x^{4}=x^{2}$
C.$(x^{3})^{3}=x^{6}$
D.$(-2xy)^{2}=4x^{2}y^{2}$
D
)A.$x^{3}· x^{4}=x^{12}$
B.$x^{8}÷ x^{4}=x^{2}$
C.$(x^{3})^{3}=x^{6}$
D.$(-2xy)^{2}=4x^{2}y^{2}$
答案:
30.D
31.下列因式分解正确的是 (
A.$-x^{2}+y^{2}=(x+y)(x-y)$
B.$a^{3}+2a^{2}b+ab^{2}=a(a+b)^{2}$
C.$x^{2}-2x+4=(x-1)^{2}+3$
D.$ax^{2}-9=a(x+3)(x-3)$
B
)A.$-x^{2}+y^{2}=(x+y)(x-y)$
B.$a^{3}+2a^{2}b+ab^{2}=a(a+b)^{2}$
C.$x^{2}-2x+4=(x-1)^{2}+3$
D.$ax^{2}-9=a(x+3)(x-3)$
答案:
31.B
32.若$x^{2}-mx+16$是完全平方式,则$m$的值为 (
A.$2$
B.$4$或$-4$
C.$2$或$-2$
D.$8$或$-8$
D
)A.$2$
B.$4$或$-4$
C.$2$或$-2$
D.$8$或$-8$
答案:
32.D
33.已知$a-b=b-c=2$,$a^{2}+b^{2}+c^{2}=11$,则$ab+bc+ac=$
A.$-22$
B.$-1$
C.$7$
D.$11$
A.$-22$
B.$-1$
C.$7$
D.$11$
答案:
33.B [解析]
∵a - b = b - c = 2,
∴a - c = 4,
∴$a² + b² + c² - ab - bc - ac = \frac{1}{2}(2a² + 2b² + 2c² - 2ab - 2bc - 2ac) = \frac{1}{2}[(a - b)² + (b - c)² + (c - a)²] = 12,$
∴ab + bc + ac = a² + b² + c² - 12 = -1.故选B.
∵a - b = b - c = 2,
∴a - c = 4,
∴$a² + b² + c² - ab - bc - ac = \frac{1}{2}(2a² + 2b² + 2c² - 2ab - 2bc - 2ac) = \frac{1}{2}[(a - b)² + (b - c)² + (c - a)²] = 12,$
∴ab + bc + ac = a² + b² + c² - 12 = -1.故选B.
34.已知$m^{2}=3n+a$,$n^{2}=3m+a$,$m$为常数,且$m\neq n$,则$m^{2}+2mn+n^{2}$的值为 (
A.$9$
B.$6$
C.$4$
D.$12$
A
)A.$9$
B.$6$
C.$4$
D.$12$
答案:
34.A [解析]
∵m² = 3n + a,n² = 3m + a,
∴m² - n² = 3n - 3m,
∴(m + n)(m - n) + 3(m - n) = 0,
∴(m - n)[(m + n) + 3] = 0.
∵m ≠ n,
∴(m + n) + 3 = 0,
∴m + n = -3,
∴m² + 2mn + n² = (m + n)² = (-3)² = 9.故选A.
∵m² = 3n + a,n² = 3m + a,
∴m² - n² = 3n - 3m,
∴(m + n)(m - n) + 3(m - n) = 0,
∴(m - n)[(m + n) + 3] = 0.
∵m ≠ n,
∴(m + n) + 3 = 0,
∴m + n = -3,
∴m² + 2mn + n² = (m + n)² = (-3)² = 9.故选A.
35.若$3^{m}=a$,$27^{n}=b$,$m$,$n$为正整数,则$3^{2m+6n}$的值为
a²b²
.
答案:
35.a²b²
36.多项式$ax^{2}-a$与多项式$2x^{2}-4x+2$的公因式是
x - 1
.
答案:
36.x - 1
37.因式分解:$(x-2)^{2}-2+x=$
(x - 2)(x - 1)
.
答案:
37.(x - 2)(x - 1)
38.已知$P=3xy-8x+1$,$Q=x-2xy-2$,当$x\neq0$时,$3P-2Q=7$恒成立,则$y$的值为
2
.
答案:
38.2 [解析]
∵P = 3xy - 8x + 1,Q = x - 2xy - 2,3P - 2Q = 7恒成立,
∴3P - 2Q = 3(3xy - 8x + 1) - 2(x - 2xy - 2) = 7,
∴9xy - 24x + 3 - 2x + 4xy + 4 = 7,13xy - 26x = 0,13x(y - 2) = 0.
∵x ≠ 0,
∴y - 2 = 0,
∴y = 2.
∵P = 3xy - 8x + 1,Q = x - 2xy - 2,3P - 2Q = 7恒成立,
∴3P - 2Q = 3(3xy - 8x + 1) - 2(x - 2xy - 2) = 7,
∴9xy - 24x + 3 - 2x + 4xy + 4 = 7,13xy - 26x = 0,13x(y - 2) = 0.
∵x ≠ 0,
∴y - 2 = 0,
∴y = 2.
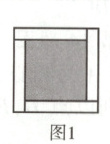
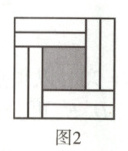
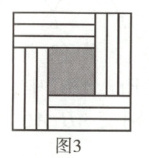
39.用若干个形状、大小完全相同的长方形纸片围成正方形:用$4$个长方形纸片围成如图$1$所示的正方形,其阴影部分的面积为$100$;用$8$个长方形纸片围成如图$2$所示的正方形,其阴影部分的面积为$81$.用$12$个长方形纸片围成如图$3$所示的正方形,其阴影部分的面积为
64
.


答案:
39.64 [解析]设长方形的长为a,宽为b,由题图1得,(a - b)² = 100,即a - b = 10①.由题图2得,(a - 2b)² = 81,即a - 2b = 9②.根据①②,解得a = 11,b = 1.由题图3得,(a - 3b)² = 64,即阴影部分的面积为64.
40.新定义一种运算:$a@b=(a+b)^{2}-(a-b)^{2}$.下面给出关于这种运算的几个结论:①$1@(-2)=-8$;②$a@b=b@a$;③若$a@b=0$,则$a$一定为$0$;④若$a+b=0$,那么$(a@a)+(b@b)=8a^{2}$.其中正确的结论是
①②④
.
答案:
40.①②④ [解析]1@( - 2) = (1 - 2)² - (1 + 2)² = -8,故①正确;a@b = (a + b)² - (a - b)² = 4ab,b@a = (b + a)² - (b - a)² = 4ab,所以a@b = b@a,故②正确;若a@b = 4ab = 0,则a,b至少有一个为0,故③不正确;若a + b = 0,那么(a@a) + (b@b) = 4a² + 4a² = 8a²,故④正确.综上所述,正确结论的是①②④.
查看更多完整答案,请扫码查看


