《2025年昕金立文化单元金卷八年级数学上册人教版》

17.(9 分)因式分解:
(1)$-2x^3 + 4x^2 - 2x$;
(2)$9a^2(x - y) + 4b^2(y - x)$;
(3)$m^2(m - 1) + 4(1 - m)$.

答案： 解:
(1)原式$=-2x(x^{2}-2x + 1)=-2x(x - 1)^{2}$.
(2)原式$=(x - y)(9a^{2}-4b^{2})=(x - y)(3a + 2b)(3a-2b)$.
(3)原式$=m^{2}(m - 1)-4(m - 1)=(m - 1)(m^{2}-4)=(m - 1)(m + 2)(m - 2)$.

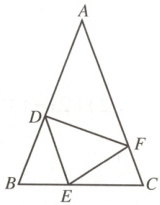
18.(9 分)如图,在△ABC 中,$AB = AC$,点 D,E,F 分别在 AB,BC,AC 边上,且$BE = CF$,$BD = CE$.
(1)求证:△DEF 是等腰三角形;
(2)当$∠A = 40^{\circ}$时,求$∠DEF$的度数.

答案：

(1)证明：$\because AB = AC,\therefore \angle B=\angle C.$在$\triangle DBE$和$\triangle ECF$中，$\begin{cases}BE = CF\\\angle B=\angle C\\BD = CE\end{cases}$，$\therefore \triangle DBE\cong\triangle ECF(SAS)$，$\therefore DE = EF$，$\therefore \triangle DEF$是等腰三角形.
(2)解：$\because \triangle DBE\cong\triangle ECF$，$\therefore \angle 1=\angle 3.$
$\because \angle A+\angle B+\angle C=180°$，$\angle A = 40°$，$\angle B=\angle C$，$\therefore \angle B=\frac{1}{2}(180°-40°)=70°$，$\therefore \angle 1+\angle 2=110°$，$\therefore \angle 3+\angle 2=110°$，$\therefore \angle DEF=70°.$

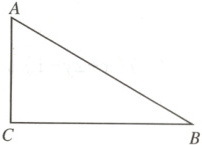
19.(9 分)如图,在 Rt△ABC 中,$∠ACB = 90^{\circ}$,$∠B = 30^{\circ}$.
(1)尺规作图:在线段 AB 上作一点 D,使得$CD = BD$(不写作法,保留作图痕迹);
(2)若点 D 到直线 BC 的距离为 2 cm,求 AD 的长.

答案：
解：
(1)如图，点$D$即为所求作.
(2)设$BC$的中点为$E.$由题意可得，$DE\perp BC$，$DE=2cm$，$\angle A=90°-\angle B=60°.\because CD = BD$，$\therefore \angle DCB=\angle B=30°$，$\therefore \angle ADC=\angle DCB+\angle B=60°$，$\because \angle ACB=90°$，$\therefore \angle ACD=60°$，$\therefore \triangle ACD$为等边三角形，$\therefore AD = CD.$在$Rt\triangle CDE$中，$CD = 2DE=4cm$，$\therefore AD = 4cm.$