《2025年昕金立文化单元金卷八年级数学上册人教版》

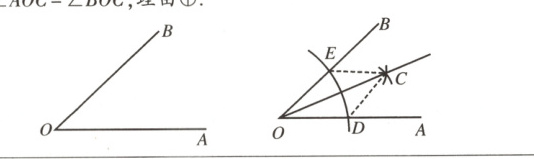
7.(郑州期末)数学课上,小明用尺规在黑板上作∠AOB的平分线，并进行简单的说明.下面是小明的解答过程，则符号♡、◇、☆、⊕代表的内容错误的是 ( )
已知:∠AOB.求作:射线OC,使∠AOC = ∠BOC.
作法:(1)以点O为圆心,在OA和OB上分别截取OD,OE,使♡;(2)分别以点D,E为圆心、以◇为半径作弧,两弧在∠AOB内交于点C;(3)作射线OC.OC就是∠AOB的平分线.
理由:(1)连接EC,DC,则EC = DC,易知△OEC≌△ODC,理由☆;
(2)所以∠AOC = ∠BOC,理由⊕.

A.♡表示“OD = OE”
B.◇表示“大于$\frac{1}{2}DE$的长”
C.☆表示“SAS”
D.⊕表示“全等三角形的对应角相等”

答案： 7.C

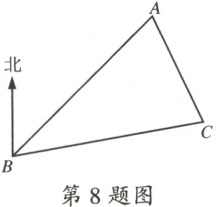
8.(新乡月考)如图,B处在A处的南偏西45°方向,C处在A处的南偏东15°方向,C处在B处的北偏东80°方向,则∠ACB = (B)

A.95°
B.85°
C.75°
D.65°

答案： 8.B

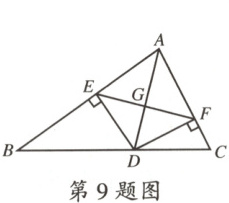
9.(濮阳期中)如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别为点E,F,连接EF,EF与AD相交于点G,则下列关系正确的是 (B)

A.AG = DG
B.AD⊥EF且EG = FG
C.DE⊥DF
D.DE//AC

答案： 9.B

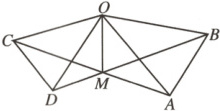
10.如图,在△OAB和△OCD中,OA = OB,OC = OD,OA＞OC,∠AOB = ∠COD = 40°,连接AC,BD交于点M,连接OM.下列结论:①AC = BD;
②∠AMB = 40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为 (B)


A.4
B.3
C.2
D.1

答案： 10.B
[解析]
∵∠COD = ∠AOB = 40°，
∴∠COD + ∠AOD = ∠AOB + ∠AOD，即∠AOC = ∠BOD。又
∵OA = OB，OC = OD，
∴△AOC ≌ △BOD，
∴∠OCA = ∠ODB，AC = BD，∠OAC = ∠OBD，故①正确。
∵∠AMB + ∠OAC = ∠AOB + ∠OBD，
∴∠AMB = ∠AOB = 40°，故②正确。
过点O作OG⊥MC于点G，OH⊥MB于点H，则∠OGC = ∠OHD = 90°，易得△OCG ≌ △ODH，
∴OG = OH，
∴MO平分∠BMC，故④正确。
根据已知条件无法得出OM平分∠BOC，故③不正确。
综上所述，正确的个数为3，故选B。

11.在△ABC中,∠A = 68°,∠B = 22°,则△ABC是直角 三角形.(填“锐角”“直角”或“钝角”)

答案： 11.直角