第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
6.如图,在等边三角形 ABC 中,点 D 是 BC 的中点,$DE ⊥ AC$于点 E,$EF ⊥ AB$于点 F,已知$BC = 16$,则 BF 的长为 (
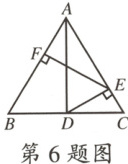
A.4
B.6
C.8
D.10
D
)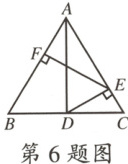
A.4
B.6
C.8
D.10
答案:
D 【解析】$\because \triangle ABC$是等边三角形,$\therefore \angle C=\angle BAC=60°,AC=AB=BC=16.\because DE\perp AC,\therefore \angle CDE=90°-\angle C=30°,\therefore CE=\frac{1}{2}CD.\because CD=\frac{1}{2}BC,\therefore CE=\frac{1}{4}BC=4,\therefore AE=AC-CE=12.\because EF\perp AB$于点$F,\therefore \angle AEF=90°-\angle EAF=30°,\therefore AF=\frac{1}{2}AE=6,\therefore BF=AB-AF=10.$故选D.
7.如图,在钝角三角形 ABC 中,∠ABC 为钝角,以点 B 为圆心,AB 长为半径画弧;再以点 C 为圆心,AC 长为半径画弧;两弧交于点 D,连接 AD,BD,CD,CB 的延长线交 AD 于点 E.下列结论错误的是 (
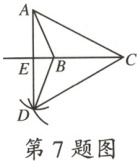
A.CE 垂直平分 AD
B.CE 平分∠ACD
C.△ABD 是等腰三角形
D.△ACD 是等边三角形
D
)
A.CE 垂直平分 AD
B.CE 平分∠ACD
C.△ABD 是等腰三角形
D.△ACD 是等边三角形
答案:
D
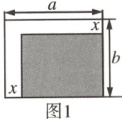
8.通过计算比较图 1,图 2 中阴影部分的面积,可以验证的计算式子是 (
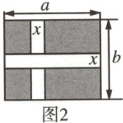
A.$a(b - x) = ab - ax$
B.$b(a - x) = ab - bx$
C.$(a - x)(b - x) = ab - ax - bx$
D.$(a - x)(b - x) = ab - ax - bx + x^2$
D
)

A.$a(b - x) = ab - ax$
B.$b(a - x) = ab - bx$
C.$(a - x)(b - x) = ab - ax - bx$
D.$(a - x)(b - x) = ab - ax - bx + x^2$
答案:
D
9.由$m(a + b + c) = ma + mb + mc$,可得$(a + b)(a^2 - ab + b^2) = a^3 - a^2b + ab^2 + a^2b - ab^2 + b^3 = a^3 + b^3$,即$(a + b)(a^2 - ab + b^2) = a^3 + b^3$①.我们把等式①叫作多项式乘法的立方公式.下列应用这个立方公式进行的变形错误的是 (
A.$(x + 4y)(x^2 - 4xy + 16y^2) = x^3 + 64y^3$
B.$(a + 1)(a^2 + a + 1) = a^3 + 1$
C.$(2x + y)(4x^2 - 2xy + y^2) = 8x^3 + y^3$
D.$x^3 + 27 = (x + 3)(x^2 - 3x + 9)$
B
)A.$(x + 4y)(x^2 - 4xy + 16y^2) = x^3 + 64y^3$
B.$(a + 1)(a^2 + a + 1) = a^3 + 1$
C.$(2x + y)(4x^2 - 2xy + y^2) = 8x^3 + y^3$
D.$x^3 + 27 = (x + 3)(x^2 - 3x + 9)$
答案:
B
10.如图,在△ABC 中,$∠BAC = 90^{\circ}$,$∠ABC = 2∠C$,BE 平分$∠ABC$交 AC 于点 E,$AD ⊥ BE$于点 D.有下列结论:①$AC - BE = AE$;②点 E 在线段 BC 的垂直平分线上;③$∠DAE = ∠C$;④$BC = 3AD$.其中正确的有 (
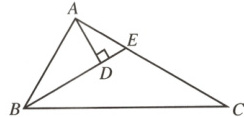
A.4 个
B.3 个
C.2 个
D.1 个
B
)
A.4 个
B.3 个
C.2 个
D.1 个
答案:
B
11.(南阳期中)计算:$(\frac{4}{5})^{2024} × (-1.25)^{2025} =$
−$\frac{5}{4}$
.
答案:
−$\frac{5}{4}$
12.如图,在四边形 ABCD 中,$AD // BC$,直线 l 是它的对称轴,$∠B = 53^{\circ}$,则$∠D =$
!img
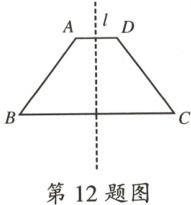
127°
.!img

答案:
127°
查看更多完整答案,请扫码查看


