《2025年昕金立文化单元金卷八年级数学上册人教版》

23.(11分)(漯河期中)【问题情境】
利用角平分线构造全等三角形是常用的方法，如图1，$OP$平分$\angle MON$，点$A$为$OM$上一点，过点$A$作$AC\perp OP$，垂足为$C$，延长$AC$交$ON$于点$B$，可根据$ASA$证明$\triangle AOC\cong\triangle BOC$，则$AO=BO$，$AC=BC$(即点$C$为$AB$的中点).
【问题探究】
(1)如图2，在$\triangle ABC$中，$AB=AC$，$\angle BAC=90^{\circ}$，$CD$平分$\angle ACB$，$BE\perp CD$，垂足$E$在$CD$的延长线上，试探究$BE$和$CD$的数量关系，并证明你的结论.
【拓展延伸】
(2)如图3，在$\triangle ABC$中，$AB=AC$，$\angle BAC=90^{\circ}$，点$D$在线段$BC$上，且$\angle BDE=\frac{1}{2}\angle C$，$BE\perp DE$于$E$，$DE$交$AB$于$F$，试探究$BE$和$DF$的数量关系，并证明你的结论.

答案：
23.解：
(1)$BE=\frac{1}{2}CD$.
证明：如图1，延长BE交CA的延长线于点F.
∵CD平分∠ACB，
∴∠FCE=∠BCE.
又∠CEF=∠CEB=90°，CE=CE，
∴△CEF≅△CEB，
∴FE=BE.
∴$BE=\frac{1}{2}BF$.
∵∠DAC=∠CEF=90°，
∴∠ACD+∠F=∠ABF+∠F=90°，
∴∠ACD=∠ABF.
∵AC=AB，∠CAD=∠BAF=90°，
∴△ACD≅△ABF，
∴CD=BF，
∴$BE=\frac{1}{2}CD$.

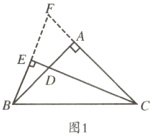
(2)$BE=\frac{1}{2}DF$，
证明：如图2，过点D作DG//CA，交BE的延长线于点G，与AF相交于点H.
∵DG//AC，
∴∠GDB=∠C，∠BHD=∠A=90°.
∵$∠BDE=\frac{1}{2}∠C$，
∴∠BDE=∠GDE=$\frac{1}{2}∠C$.
∵BE⊥DE，
∴∠BED=∠GED=90°，
∴∠BED=∠BHD.又∠EFB=∠HFD，
∴∠EBF=∠HDF.
∵AB=AC，∠BAC=90°，
∴∠C=∠ABC=45°.
∵GD//AC，
∴∠GDB=∠C=45°，
∴∠GDB=∠ABC=45°，
∴BH=DH.又∠BHG=∠DHF=90°，
∴△BHG≅△DHF，
∴BG=DF.
∵∠BDE=∠GDE，∠BED=∠GED，
∴△BDE≅△GDE，
∴BE=GE，
∴$BE=\frac{1}{2}BG=\frac{1}{2}DF$.