《2025年昕金立文化单元金卷八年级数学上册人教版》

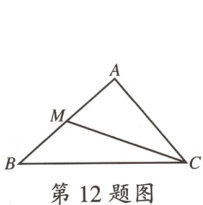
12.(驻马店月考)如图，CM 是△ABC 的中线，BC = 8 cm，若△BCM 的周长比△ACM 的周长大 3 cm，则 AC 的长为5cm.

答案： 12.5cm

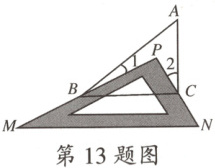
13.如图，在△ABC 中，有一块直角三角板 PMN 放置在△ABC 上(点 P 在△ABC 内)，使三角板 PMN 的两条直角边 PM，PN 恰好分别经过点 B 和点 C. 若∠A = 52°，则∠1 + ∠2 =38°.

答案： 13.38°

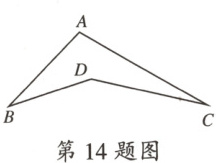
14.如图，∠BDC = 150°，∠B = $\frac{1}{3}$∠BDC，∠C = 28°，则∠A 的度数为72°.

答案： 14.72°

15.如图，△ABC 三边的中线 AD，BE，CF 交于点 G，且 AG:GD = 2:1，若$S_{\triangle ABC}=12$，则图中阴影部分的面积是4.

答案： 15.4

16.(8 分)已知 a，b，c 为△ABC 的三边长，且 b，c 满足$(b - 5)^{2}+(c - 7)^{2}=0$，a 为方程$\vert a - 3\vert=2$的解，求△ABC 的周长，并判断△ABC 的形状.

答案： 16.解:
∵(b - 5)² + (c - 7)² = 0,
∴$\begin{cases}b - 5 = 0\\c - 7 = 0\end{cases}$，解得$\begin{cases}b = 5\\c = 7\end{cases}$，
∵a为方程|a - 3| = 2的解，
∴a = 5或a = 1,当a = 1,b = 5,c = 7时，1 + 5 ＜ 7，不能组成三角形，故a = 1不符合题意.
∴a = 5,
∴△ABC的周长 = 5 + 5 + 7 = 17,
∵a = b = 5,
∴△ABC是等腰三角形.