第10页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
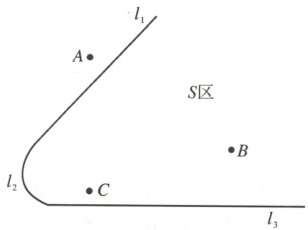
18.(9分)如图,某城市公园里有三个景点$A$,$B$,$C$,直线$l_1$,$l_3$表示直路,而$l_2$表示弯路.想在$S$区里修建一座公厕$P$,使它到两条路$l_1$和$l_3$的距离相等,且到两个景点$B$和$C$的距离也相等.求点$P$的位置.

答案:
18.解:设$l_1$和$l_3$交于点E,以点E为圆心,以适当的长为半径画弧分别交$l_1$,$l_3$于点M,N,分别以点M,N为圆心,以大于$\frac{1}{2}$MN的长为半径画弧,在$l_1$,$l_3$的内部交于点F,作射线EF,连接BC,分别以点B,C为圆心,以大于$\frac{1}{2}$BC的长为半径画弧,两弧交于点T,H,作直线TH与射线EF交于点P,则点P为所求作的点.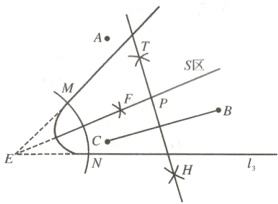
理由如下:
由作图可知:EF为直线$l_1$,$l_3$夹角的平分线,点P在EF上,
∴点P到$l_1$和$l_3$的距离相等,
由作图可知:直线TH为线段BC的垂直平分线,点P在TH上,
∴TB=TC.
∴点P到$l_1$和$l_3$的距离相等,且到点B和C的距离也相等.
18.解:设$l_1$和$l_3$交于点E,以点E为圆心,以适当的长为半径画弧分别交$l_1$,$l_3$于点M,N,分别以点M,N为圆心,以大于$\frac{1}{2}$MN的长为半径画弧,在$l_1$,$l_3$的内部交于点F,作射线EF,连接BC,分别以点B,C为圆心,以大于$\frac{1}{2}$BC的长为半径画弧,两弧交于点T,H,作直线TH与射线EF交于点P,则点P为所求作的点.

理由如下:
由作图可知:EF为直线$l_1$,$l_3$夹角的平分线,点P在EF上,
∴点P到$l_1$和$l_3$的距离相等,
由作图可知:直线TH为线段BC的垂直平分线,点P在TH上,
∴TB=TC.
∴点P到$l_1$和$l_3$的距离相等,且到点B和C的距离也相等.
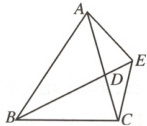
19.(9分)如图,$BD$为$\triangle ABC$的角平分线,且$BD=BC$,$E$在$BD$的延长线上,$BE=BA$,连接$AE$,$CE$.求证:
(1)$\triangle ABD\cong\triangle EBC$;
(2)$\angle BCE+\angle BCD=180^{\circ}$.
(1)$\triangle ABD\cong\triangle EBC$;
(2)$\angle BCE+\angle BCD=180^{\circ}$.

答案:
19.证明:
(1)
∵BD为△ABC的角平分线,
∴∠ABD=∠EBC.
又
∵BD=BC,BA=BE,
∴△ABD≅△EBC.
(2)由
(1)得△ABD≅△EBC,
∴∠BDA=∠BCE.
∵BD=BC,
∴∠BDC=∠BCD.
又∠BDA+∠BDC=180°,
∴∠BCE+∠BCD=180°.
(1)
∵BD为△ABC的角平分线,
∴∠ABD=∠EBC.
又
∵BD=BC,BA=BE,
∴△ABD≅△EBC.
(2)由
(1)得△ABD≅△EBC,
∴∠BDA=∠BCE.
∵BD=BC,
∴∠BDC=∠BCD.
又∠BDA+∠BDC=180°,
∴∠BCE+∠BCD=180°.
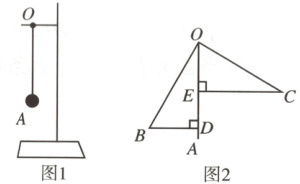
20.(9分)(洛阳期末)在一个支架的横杆点$O$处用一根绳悬挂一个小球$A$,小球$A$可以摆动,如图1,$OA$表示小球静止时的位置.如图2,当小球从$OA$摆到$OB$位置时,过点$B$作$BD\perp OA$于点$D$,当小球摆到$OC$位置时,$OB$与$OC$恰好垂直,过点$C$作$CE\perp OA$于点$E$,测得$CE=24\ {cm}$,$OA=OB=OC=30\ {cm}$.
(1)试说明$OE=BD$;
(2)求$AD$的长.
(1)试说明$OE=BD$;
(2)求$AD$的长.

答案:
20.解:
(1)
∵OB⊥OC,
∴∠BOD+∠COE=90°.
∵CE⊥OA,BD⊥OA,
∴∠CEO=∠ODB=90°,
∴∠BOD+∠B=90°,∠COE=∠B,又OC=BO,
∴△COE≅△OBD,
∴OE=BD.
(2)
∵△COE≅△OBD,
∴CE=OD=24cm.
∵OA=30cm,
∴AD=OA-OD=30-24=6(cm).
(1)
∵OB⊥OC,
∴∠BOD+∠COE=90°.
∵CE⊥OA,BD⊥OA,
∴∠CEO=∠ODB=90°,
∴∠BOD+∠B=90°,∠COE=∠B,又OC=BO,
∴△COE≅△OBD,
∴OE=BD.
(2)
∵△COE≅△OBD,
∴CE=OD=24cm.
∵OA=30cm,
∴AD=OA-OD=30-24=6(cm).
查看更多完整答案,请扫码查看


